Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivada De Logaritmo

Ver Todos os Exercícios

Teoria

Fala aí! Hoje a gente vai aprender calcular a derivada de um logaritmo, mas não para por aí…vamos descobrir como usar a derivada de log pra resolver derivadas que não são logarítmicas!

-Ué, mas porque eu faria isso?! 😖😖😖

Pra facilitar a sua vida! A gente vai usar as propriedades dos logaritmos pra fugir de algumas regras do produto e do quociente. E venhamos e convenhamos, em cálculo é sempre bom ter uma cartinha na manga! 😄 😉

Como Calcular a Derivada de um Logaritmo?

Para fazer a derivação logarítmica, usamos a seguinte fórmula:

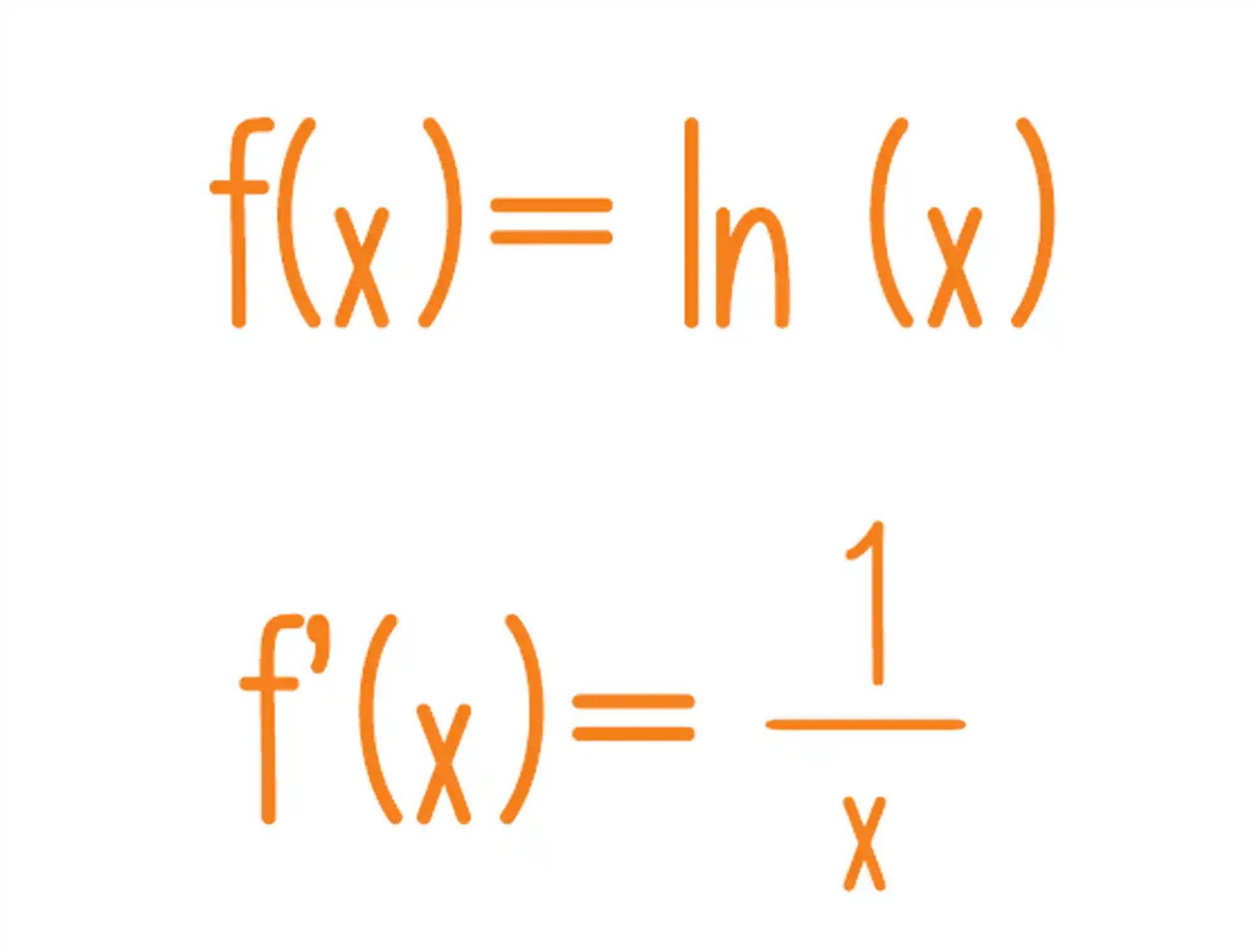
Derivada de logaritmo neperiano
Derivada de logaritmo neperiano

Acima temos a derivada do logaritmo neperiano, mas e se a gente topar com um log em outra base?

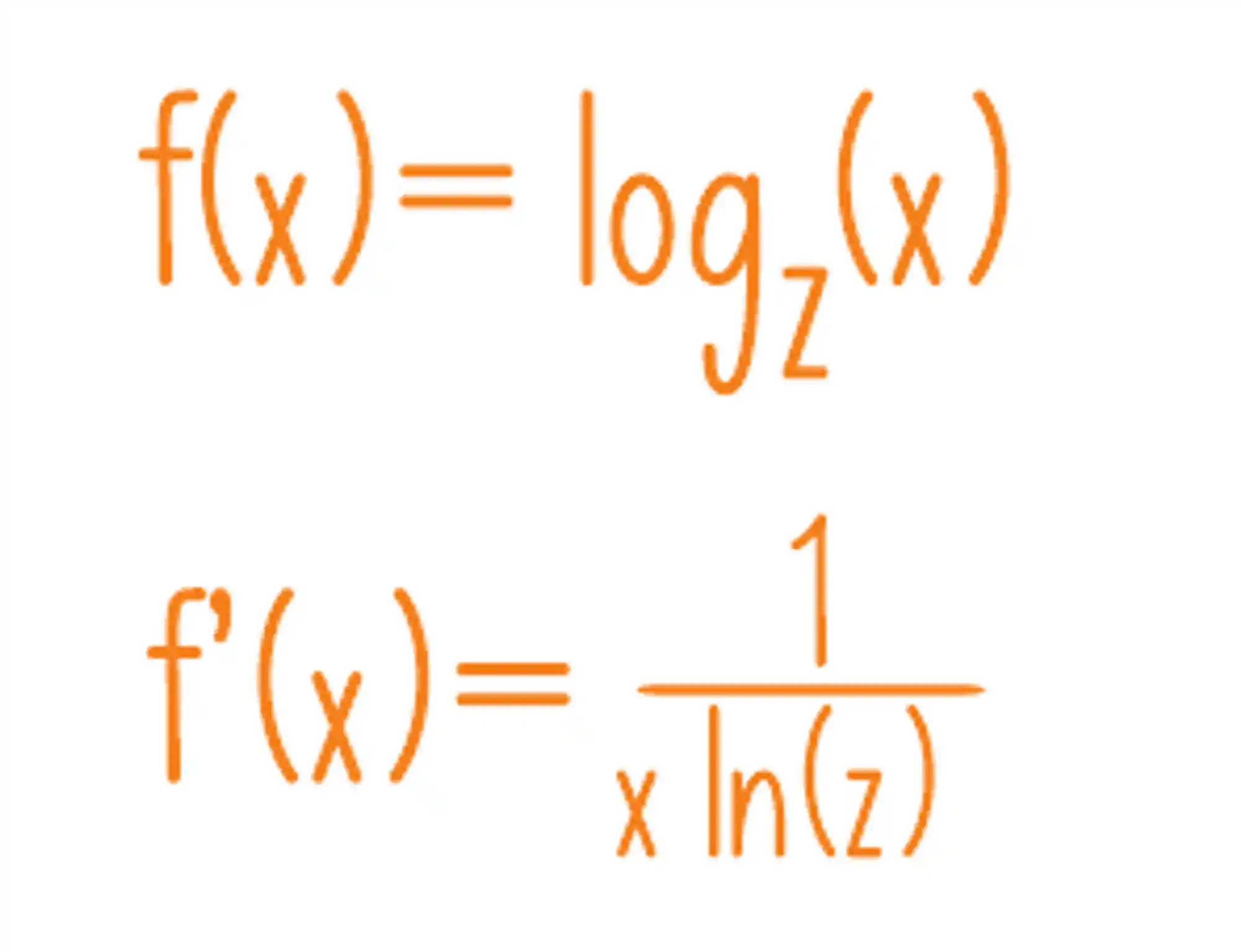
Derivada de log
Derivada de log

Aqui não tem muito mistério, é só decorar mesmo! Mas é claro, em cálculo sempre dá pra complicar, bora ver um exemplo de como isso pode aparecer nos exercícios? 🤩

📢 Clique para saber mais:

Exemplo: Calcule a Derivada de

Pra resolver esse exemplo a gente vai juntar a derivada de logaritmo com a regra da cadeia! Temos a nossa função:

Definimos :

Agora a gente vai derivar essa galera:

Aplicamos a regra da cadeia:

Damos aquela arrumadinha e prontinho:

Você também pode conferir esse conteúdo em vídeo:

Exemplo: Derive usando derivada logarítmica

-QUEEE??? MAS ESSA FUNÇÃO NEM TEM LOG! 😲😲😲😲

Passo 1 : Multiplicar os dois lados por

Ficamos com:

Passo 2 : Usamos as propriedades de logaritmo

Aqui vamos usar a propriedade do peteleco:

Passo 3: Derivamos os dois lados usando a derivada implícita

Resolvendo, temos:

Passo 4: Isolar y’ e substituir y na equação pela função original;

Lembrando que , então:

Prontinho. Temos a nossa derivada! Agora vamos praticar com mais exercícios?

Exemplo: Derive usando derivada logarítmica

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.221-89

No exercício, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada:

y = x + 1 x

Passo 1

Como o enunciado nos pediu, vamos usar a derivada logarítmica. Então, primeiro vamos aplicar o logaritmo dos dois lados

ln ⁡ y = ln ⁡ x + 1 x

Passo 2

Pela propriedade do logaritmo, temos:

ln ⁡ x + 1 x = x ln ⁡ x + 1

Passo 3

Então queremos achar a derivada:

ln ⁡ y ' = x ln ⁡ x + 1 '

Derivamos pela Regra do Produto a função de x e usamos a derivada implícita na função de y :

y ' y = x ' ln ⁡ x + 1 + x ln ⁡ x + 1 '

Usando a regra da cadeia para o termo ln ⁡ ( x + 1 ) , temos

y ' = y 1 ln ⁡ x + 1 + x x + 1 ' x + 1

= y ln ⁡ x + 1 + x x + 1

Passo 4

Substituindo o y de volta:

y = x + 1 x

y ' = x + 1 x ln ⁡ x + 1 + x x + 1

Resposta

y ' = x + 1 x ln ⁡ x + 1 + x x + 1

Exercício Resolvido #2

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.220-47

No exercício, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada:

y = t t + 1 t + 2

Passo 1

O enunciado pediu para usar derivação logarítmica. Então, aplicando o logaritmo em ambos os lados, teremos:

ln ⁡ y = ln ⁡ t t + 1 t + 2

Passo 2

Pela propriedade do logaritmo, teremos:

ln ⁡ t t + 1 t + 2 = ln ⁡ t + ln ⁡ t + 1 + ln ⁡ t + 2

Passo 3

Derivaremos agora,

ln ⁡ y ' = ln ⁡ t + ln ⁡ t + 1 + ln ⁡ t + 2 '

Derivamos pela Regra da cadeia os termos ln ⁡ ( t + 1 ) e ln ⁡ ( t + 2 ) , obtendo:

y ' y = t ' t + t + 1 ' t + 1 + t + 2 ' t + 2

y ' = y 1 t + 1 t + 1 + 1 t + 2

Passo 4

Substituindo o y de volta:

y = t t + 1 t + 2

y ' = t t + 1 t + 2 1 t + 1 t + 1 + 1 t + 2

Se quiser pode fazer a distributiva

y ' = t + 1 t + 2 + t t + 2 + t t + 1

Resposta

y ' = t + 1 t + 2 + t t + 2 + t t + 1

Exercício Resolvido #3

UNICAMP - Cálculo 1 - P2 2013.1 – 3

Use a diferenciação logarítmica para determinar a derivada da função:

y = y x = cos ⁡ x sen ⁡ x   ,             0 < x < π 2

Passo 1

Vamos lá, seguimos o que ele pediu: diferenciação logarítmica. É um processo que não tem nada demais, basta lançar o logaritmo na igualdade:

ln ⁡ y x = ln ⁡ cos ⁡ x sen ⁡ x

Passo 2

Vamos usar as propriedades do logaritmo:

ln ⁡ y x = sen ⁡ x ln ⁡ ( cos ⁡ x )

Passo 3

Agora fazemos uma derivação implícita do lado esquerdo e usamos a Regra do Produto e a Regra da Cadeia do lado direito.

ln ⁡ y x ' = sen ⁡ x ln ⁡ cos ⁡ x '

1 y x y ' x = cos ⁡ x ln ⁡ cos ⁡ x + sen ⁡ x 1 cos ⁡ x ( - sen ⁡ x )

Passo 4

Repara que se passarmos y ( x ) para o outro lado teremos a derivada, que é o que o foi pedido lá em cima. Então, sabendo que y x = cos ⁡ x sen ⁡ x , passamos ele multiplicando:

y ' x = cos ⁡ x sen ⁡ x cos ⁡ x ln ⁡ cos ⁡ x + sen ⁡ x 1 cos ⁡ x - sen ⁡ x

y ' x = cos ⁡ x sen ⁡ x cos ⁡ x ln ⁡ cos ⁡ x - sen 2 ⁡ x cos ⁡ x

É esse troço feio aí o resultado!

Resposta

y ' x = cos ⁡ x sen ⁡ x cos ⁡ x ln ⁡ cos ⁡ x - sen 2 ⁡ x cos ⁡ x

Exercício Resolvido #4

UNICAMP - Cálculo 1 - Exame 2012 Diurno - 1 b

Seja f x = ln ⁡ 3 π x sen ⁡ 2 x . Determine:

f ' π

Passo 1

Vamos derivar esse cara com o auxílio da derivação implícita. Então, vamos usar o seguinte:

f x = e ln ⁡ f x

Para o nosso caso vamos ficar com:

f x = e ln ⁡ ln ⁡ 3 π x sen ⁡ 2 x

Passo 2

As propriedades vão simplificar o cara aqui:

e ln ⁡ ln ⁡ 3 π x sen ⁡ 2 x = e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x

Passo 3

Nessa situação, podemos derivar a função exponencial, sabendo que ela pede, pela Regra da Cadeia, a derivada do seu expoente. Para derivar esse expoente, por sua vez, a gente precisa chamar a Regra do produto.

Fazendo então:

f ' x = e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x '

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x '

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x sen ⁡ 2 x ' ln ⁡ ln ⁡ 3 π x + sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x '

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x 2 cos ⁡ 2 x ln ⁡ ln ⁡ 3 π x + sen ⁡ 2 x ln ⁡ 3 π x ' ln ⁡ 3 π x

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x 2 cos ⁡ 2 x ln ⁡ ln ⁡ 3 π x + sen ⁡ 2 x 3 π x ' 3 π x 1 ln ⁡ 3 π x

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x 2 cos ⁡ 2 x ln ⁡ ln ⁡ 3 π x + sen ⁡ 2 x ln ⁡ 3 π x 3 π 3 π x

= e sen ⁡ 2 x ln ⁡ ln ⁡ 3 π x 2 cos ⁡ 2 x ln ⁡ ln ⁡ 3 π x + sen ⁡ 2 x x ln ⁡ 3 π x

E é essa a derivada. Pequena, né?

Passo 4

Agora, ainda não acabou. Falta substituir x = π em f ' x :

f ' π = e sen ⁡ 2 π ln ⁡ ln ⁡ 3 π π 2 cos ⁡ 2 π ln ⁡ ln ⁡ 3 π π + sen ⁡ 2 π π ln ⁡ 3 π π

= e 0 ln ⁡ ln ⁡ 3 2 1 ln ⁡ ln ⁡ 3 + 0 π ln ⁡ 3

= e 0 2 ln ⁡ ln ⁡ 3

= 2 ln ⁡ ln ⁡ 3

Resposta

f ' π = 2 ln ⁡ ln ⁡ 3

Exercício Resolvido #5

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp.221-89

No exercício, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada:

y = sin ⁡ x sinh ⁡ x

Passo 1

Como o enunciado nos pediu, vamos usar a derivada logarítmica. Então, primeiro vamos aplicar o logaritmo dos dois lados

ln ⁡ y = ln ⁡ sin ⁡ x sinh ⁡ x

Passo 2

Pela propriedade do logaritmo, temos:

ln ⁡ sin ⁡ x sinh ⁡ x = sinh ⁡ x ln ⁡ sin ⁡ x

Passo 3

Então queremos achar a derivada:

ln ⁡ y ' = sinh ⁡ x ln ⁡ sin ⁡ x '

Derivamos pela Regra do Produto a função de x e usamos a derivada implícita na função de y :

y ' y = sinh ⁡ x ' ln ⁡ sin ⁡ x + sinh ⁡ x ln ⁡ sin ⁡ x '

Usando a regra da cadeia para o termo ln ⁡ sin ⁡ x , temos

y ' = y cosh ⁡ x ln ⁡ sin ⁡ x + sinh ⁡ x sin ⁡ x ' sin ⁡ x

= y cosh ⁡ x ln ⁡ sin ⁡ x sin ⁡ x sin ⁡ x + sinh ⁡ x cos ⁡ x sin ⁡ x

Passo 4

Substituindo o y de volta:

y = sin ⁡ x sinh ⁡ x

y ' = sin ⁡ x sinh ⁡ x cosh ⁡ x ln ⁡ sin ⁡ x sin ⁡ x sin ⁡ x + sinh ⁡ x cos ⁡ x sin ⁡ x

y ' = sin ⁡ x sinh ⁡ x - 1 cosh ⁡ x ln ⁡ sin ⁡ x sin ⁡ x + sinh ⁡ x cos ⁡ x

Resposta

y ' = sin ⁡ x sinh ⁡ x - 1 cosh ⁡ x ln ⁡ sin ⁡ x sin ⁡ x + sinh ⁡ x cos ⁡ x

Exercícios de Livros Relacionados

Mostre que underset(n - oo)(lim) (1 + (x)/(n))^n = e^x , para qualquer xo
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 3 θ e - θ )
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 2 e - t sen ⁡ t )
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = x 2 + 1 x - 1 2
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = t ( t + 1 ) ( t + 2 )