Derivada da Função Inversa
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí! Bora aprender a achar a derivada da função inversa com o RespondeAí?!
-Vamos que Vamos!
Indo bem direto ao ponto!
Seja
Então tudo que temos que fazer é verificar se a função é inversível, ou seja, se ela é bijetora e se ela é derivável no seu domínio!
-Mas, você lembra o que é uma função Bijetora?!
Função Bijetora
As funções bijetoras simplesmente são aquelas que são injetoras e sobrejetoras. Só isso!
-Mas o que são funções injetoras e sobrejetoras?! 🤣🤣🤣
Em uma função injetora todos os elementos do domínio,
Essa imagem da uma traduzida nessa definição:
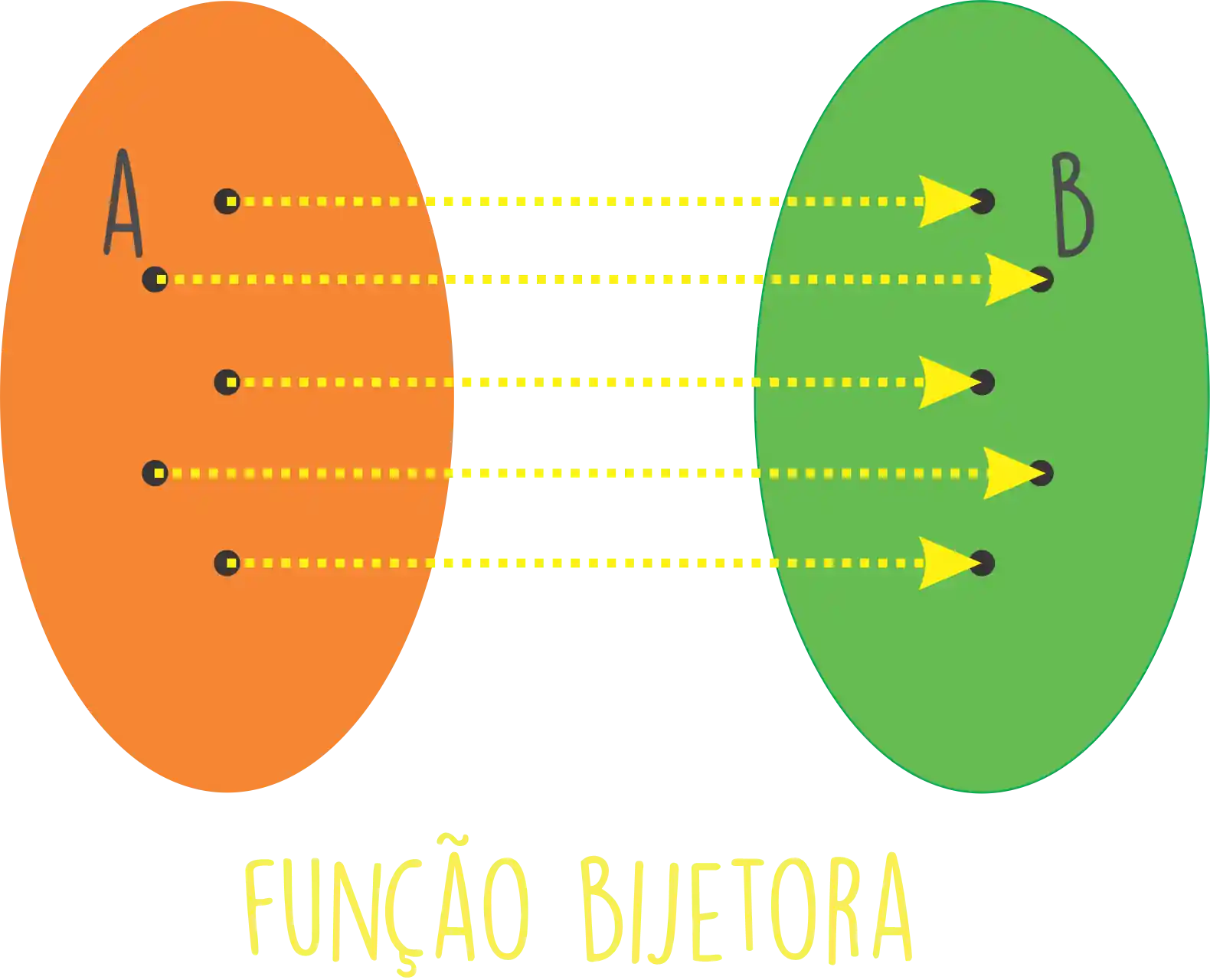
Para que uma função seja injetora e sobrejetora ao mesmo tempo todos os elementos do contradomínio
- Clique aqui para entender mais sobre: Função Injetora, Sobrejetora e Bijetora.
Calculando a Derivada da Inversa
Agora, vamos fazer um exemplo!?
Calcule a derivada da inversa para a seguinte função:
Passo 1: A função é Invertível?
Primeiro temos que descobrir se a função é invertível ou seja, se ela é bijetora! Pra facilitar podemos olhar o gráfico da função:
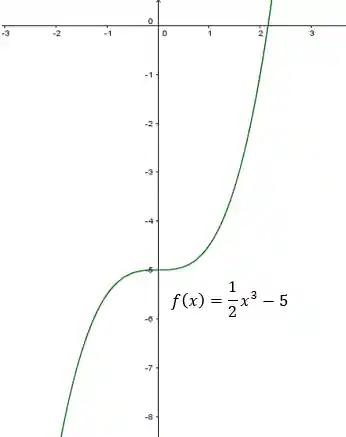
Podemos reparar que:
- A função é injetora, pois não temos dois valores de
diferentes que deem um mesmo valor de ; - e ela é sobrejetora pois ela sua imagem vai de
a , ou seja é igual aos números reais r ao seu contradomínio!
Logo a função é bijetora!
Passo 2: Calcular a função inversa e sua derivada
Temos a nossa função:
Pra acharmos a função inversa, isolamos o
E trocamos o
Agora calculamos sua derivada:
Passo 3: Substituir na Fórmula
Agora só precisamos usar a nossa formulinha:
Substituindo, temos:
Aweee!!
Agora, se liga nesse exercício resolvido em vídeo sobre derivada da função inversa que eu separei especialmente pra você:
Bora praticar com mais exercícios?
Calculando a Derivada da Inversa
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ - Cálculo B - P2 2015.1 – 3 ab - Modificada
Considere a função inversa de . Sejam , . Determine:
Determine .
Determine .
Passo 1
Ele não perguntou sobre a existência da inversa, então vamos focar só na fórmula da inversa.
Ora, se , sabemos que . O cara nos disse que a inversa de é a função , que será igual, portanto, a . Assim:
Passo 2
Se é a inversa de , nós temos que:
Queremos quando , portanto:
Do enunciado, temos que :
Resposta
Exercício Resolvido #2
PUC-RJ - Cálculo B - P4 2015.1 - 1 d
Ache , sendo a inversa de , e .
Passo 1
Ele não perguntou sobre a existência da inversa, então vamos focar só na fórmula da derivada inversa.
A derivada da inversa de uma função é dada da seguinte maneira:
Se é a inversa de , teremos:
Como vale, pela função dada:
vemos que para sua inversa valerá que . Então, pode ser calculado da seguinte maneira:
Sendo o ponto coordenado .
Passo 2
Vamos derivar para achar o :
Assim,
Resposta
Exercício Resolvido #3
PUC-RJ - Cálculo B - P2 2013.2 – 3
Seja para
A função é inversível?
Determine uma expressão pra a função , a inversa de
Calcule a derivada de em
Passo 1
Para sabermos se a função é inversível vamos usar o Teorema da Função Inversa.
É só ver se a sua derivada vai ser sempre diferente de
E vamos ter que essa derivada só vai ser em
Como esse valor não está incluído no domínio (pois ele diz que ) ela sempre vai ser diferente de . Portanto pelo teorema da função inversa ela é inversível.
Passo 2
Para descobrirmos essa expressão devemos trocar o com o e achar o novo , assim
Nos temos
Vamos isolar o
Devemos fazer alguma coisa para chegar em sozinho. Vamos fazer um negócio chamado completar quadrado. Concorda que:
certo? Então, se eu somar um de cada lado, fica assim:
Vamos ter com isso
Como ele disse que devemos ter esse cara com sinal de na raiz, já que a raiz gera um termo positivo e , onde é positivo, será menor que
Essa é a nossa função inversa
Podemos mudar agora esse por na resposta final, só para deixar bonitinho com uma função inversa de
Passo 3
Vamos aplicar o teorema da função inversa
Vamos trocar isso aí porque ele quer a derivada da inversa e temos a derivada de
Ele quer isso nos diz que vamos achar o valor de para isso
Usamos Bhaskara:
Como o valor de , vamos ter
Passo 4
Agora que sabemos o valor de podemos aplicar o teorema da função inversa
Vamos ter
A derivada de vai ser
Resposta
Exercício Resolvido #4
UFF - Cálculo IA - P2 Sérgio Almaraz 2014.2 – 2
Considere a função
Onde é uma constante.
Mostre que restrita a possui uma inversa
Determine
Determine
Determine um valor de tal que seja inversível em
Passo 1
Para sabermos se a função é inversível é só ver se a sua derivada vai ser sempre diferente de . Para , vale:
Nessa situação, a derivada vale:
Repara que a função tem derivada para todo . Significa que ela é sempre decrescente nessa faixa do domínio. Com isso, ela sempre vai ser diferente de 0. Portanto pelo teorema da função inversa ela é inversível.
A função vai ser inversível para .
Passo 2
Para determinar temos que procurar quando a função valerá
Isso pode acontecer em duas regiões: e
Não faz muito sentido olhar para esse segundo caso se não conhecemos o valor de . Então vamos focar em achar um que gere:
Na malandragem, eu fui usando alguns valores de bons de mexer, como e . Como a função é decrescente em toda essa região, como vimos na letra , se acharmos um que satisfaça esse será o único valor possível para solucionar a questão.
Por tentativa, descobriremos :
Logo,
Passo 3
Pelo derivada da Inversa, teremos:
Derivamos , fica assim:
Usando ficará:
Logo,
Passo 4
Para a função ser inversível para todo real, ela deve ser inversível nos seus dois domínios: para e para . Já provamos na que isso vale para . Vamos olhar o outro domínio.
A função aqui é
Para que seja inversível em todo o domínio precisamos ter . Nessa região a derivada é dada por:
Rapaz, repara, posso chutar qualquer valor de ali nesse cara, mas eu vou ter sempre essa derivada zerando em . No resto domínio, ela manterá o mesmo sinal de , sempre para .
Agora, em supondo algum valor de que faça da função contínua, poderíamos fazer as derivadas laterais e igualá-las:
Não importa o lado, em ambas zeram.
Enfim, a conclusão é que nenhum satisfaz isso!
Resposta
Exercício Resolvido #5
UFF - Cálculo IA - P2 Humberto 2014.2 – 2
Sejam , e funções reais de classe , com uma função inversível e
Calcule em termos de , , , e . Justifique sua resposta.
Calcule sabendo que , , , , e . Justifique sua resposta.
Passo 1
Ele não perguntou sobre a existência da inversa, então vamos focar só na fórmula da derivada inversa.
Aqui vamos usar algumas regras de derivação, primeiro a regra do quociente
Precisamos achar essas derivadas
Passo 2
Vamos começar por
Bom, temos que sua derivada será dada por:
Se
Logo, teremos
Que ficará assim:
Passo 3
Vamos para
Usamos a Regra da Cadeia para chegar nisso:
Passo 4
Recapitulando, temos
E acabamos de calcular
Substituindo isso na equação que está ali no inicio desse passo
Ficou feio, eu sei. Mas no próximo item, vamos dar nomes aos bois!
Passo 5
Ele quer a derivada em um ponto, no caso
Vamos pegar a fórmula que achamos no fim do passo e trocar por .
Usando os dados do enunciado, temos:
, , , , e .
Agora eu te pergunto, por que ele deu o valor de , se estamos interessados no ponto

Ele deu esse ponto, por que nele a função assume o valor 0! Com isso, a sua função inversa no ponto 0, vai ser o valor do ponto em que a função que deu 0. Fica assim, ó:
Sabemos também que
(Um macete aqui, é que a função e no ponto 0, assume os mesmos valores que as funções e , no ponto 0).
Passo 6
Substituindo isso tudo, teremos:
Resposta
Exercício Resolvido #6
Seja a função
Determine o maior intervalo onde é invertível.
Passo 1
A primeira coisa é tentar aplicar o Teorema da Função Inversa. Pra isso vamos derivar a função:
Igualando a zero:
Então temos ou:
O que é impossível!! Isso porque .
Ok, então o único ponto onde deu problema foi mesmo. Então garantimos que é invertível em ou em .
Mas ele quer o maior intervalo possível, vamos ver se temos a função inversível no
Passo 2
Agora resta testar se é bijetora. Se for o caso, ela será invertível em todo o .
Vamos dar uma olhada nessa função:
Hmm... Reparou alguma coisa?
Nenhum dos termos que aparece nessa função pode ser negativo! Temos que:
Opa! Isso significa que a imagem de não inclui os números negativos (nem o zero, aliás), portanto não é sobrejetora não é bijetora em todo o . Desta forma, considerando o intervalo como sendo o domínio da função, percebemos que f é bijetora neste domínio.
Essa é uma possível resposta então, se preferir, pode falar que o maior intervalo é o de pois aqui também a função é Bijetora.
PORÉM CUIDADO! A resposta é um ou outro, você quem escolhe, mas não pode ser os dois ao mesmo tempo, heim!
Resposta
Outra resposta possível: