Seja dada por .
a) Mostre que é inversível e determine sua inversa
b) Esboce os gráficos de e de
Passo 1
a) Escrevemos para obter a inversa :
Passo 2
b) Agora vamos esboçar os gráficos, com em vermelho e em azul:
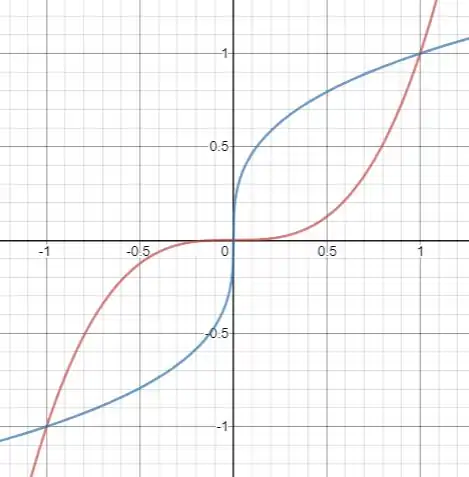
Repare que os gráficos são simétricos em relação à reta , pois uma função é inversa da outra!
Resposta
a)