Função Diferenciável
Produzido por Arthur Melo de AlmeidaTeoria
Opaa, seja muito bem vindo ao Responde Aí, seu portal de exatas mais completo! Bora descobrir o que é uma função diferenciável?!
Quando Eu Posso Derivar uma Função?
Pra a gente derivar uma função ela tem que ser diferenciável, mas…quando ela é diferenciável? Pra descobrirmos isso, temos que ter em mente alguns critérios 👇
1° Critério: Se a função não é contínua em um determinado ponto então ela NÃO É diferenciável nesse ponto.
A função contínua é aquela que você pode desenhar sem tirar o lápis da folha!
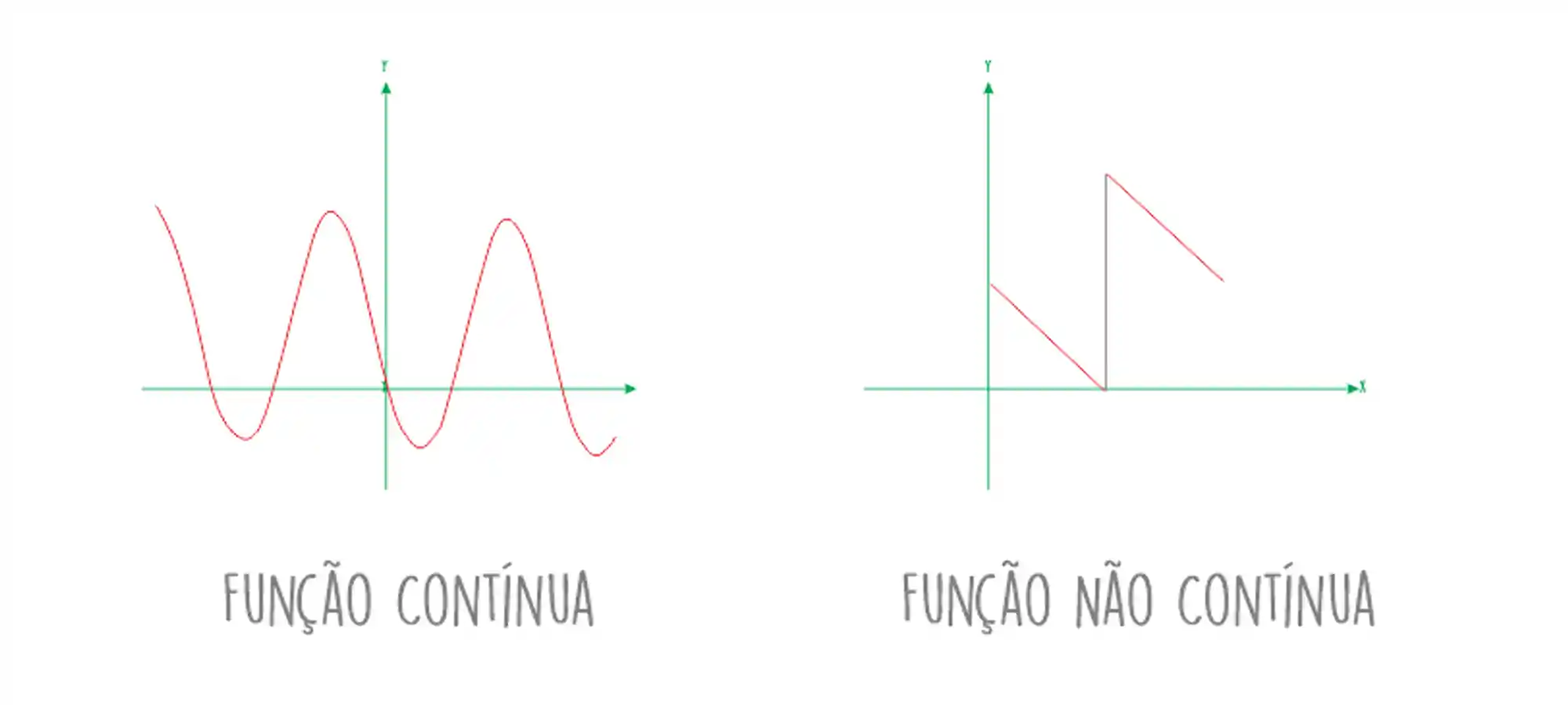
📢 Clique para saber mais:
- Função Diferenciável: Exercícios Resolvidos
- Tabela de Derivadas
- Propriedade de Derivadas
- Calculadora de Derivadas
2° Critério: Se a função é contínua em uma determinado ponto então ela será diferenciável SE as derivadas laterais nesse ponto são iguais e diferentes de
Resumidamente, uma função contínua em
E aí, para saber se uma função contínua é diferenciável num ponto qualquer, é só você achar as derivadas laterais nesse ponto e analisar 😉
Exemplo: Verifique a diferenciabilidade
A primeira coisa que temos que conferir é se a função é contínua em
Se os limites laterais são iguais, então a função é contínua! Agora derivamos cada domínio, primeiro pela direita:
Agora pela esquerda:
As derivadas batem, então a função é diferenciável no ponto