Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Modelagem Com EDO de 1° Ordem - Fator Integrante

Ver Todos os Exercícios

Teoria

Você sabia que é possível resolver vários problemas de modelagem com a nossa boa e velha EDO de primeira ordem, usando fator integrante?! Vou te mostrar alguns casos! 👇👇👇

Modelagem de um Circuito Elétrico

Uma modelagem muito comum que vamos ter são os circuitos elétricos. Aqui para chegar nas equações se usa as Leis de Kirchhoff! Aqui a gente esta interessado só na modelagem… Então se você quiser saber um pouquinho mais sobre esses circuitos dá uma conferida aqui! 😉


Nas modelagens de circuitos elétricos temos principalmente dois casos:

Circuito RL em Série

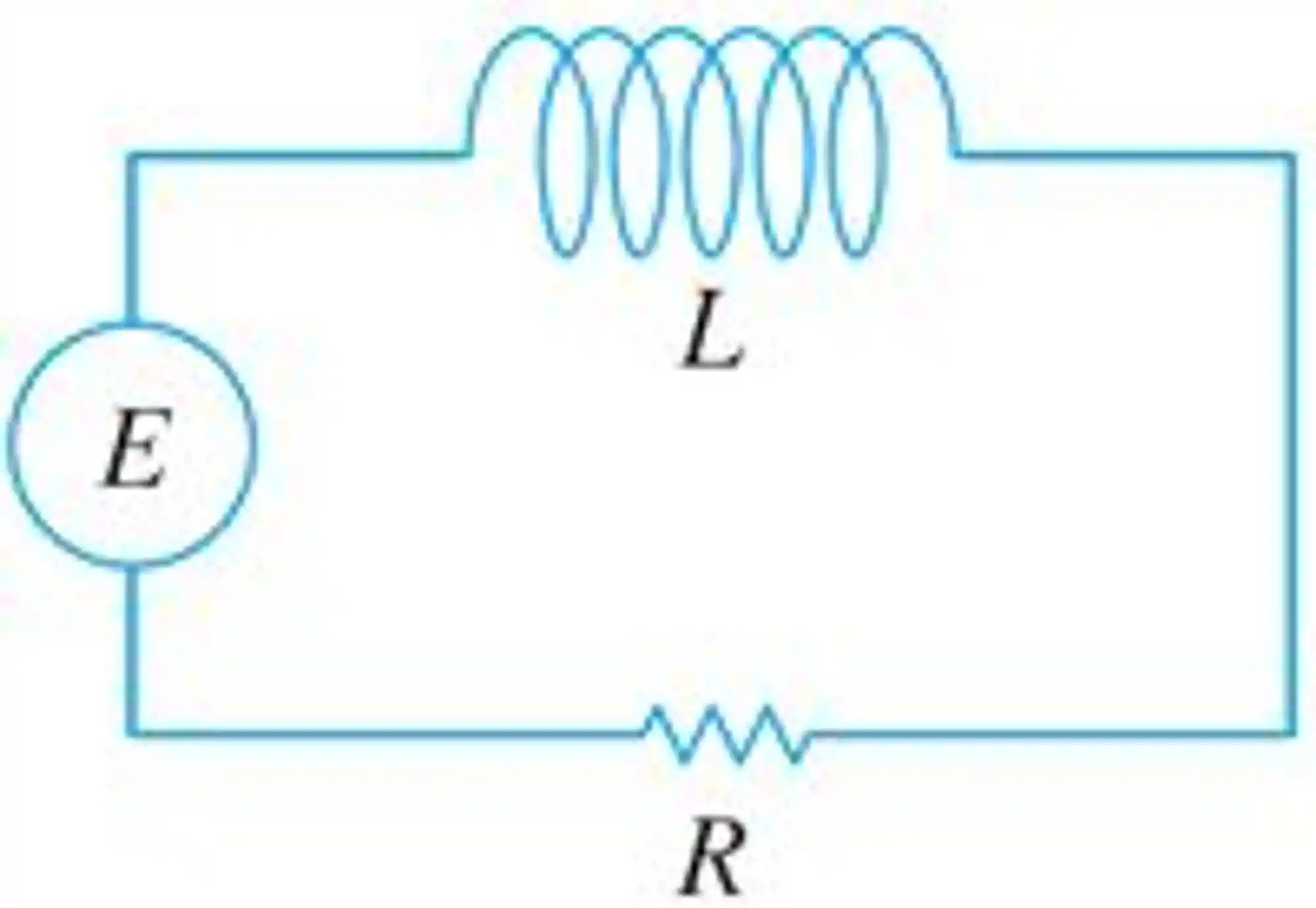
Um circuito RL é composto por um indutor e um resistor ligados em série é representado da seguinte forma:

Aqui vamos ter a EDO para chegar na função da corrente em função do tempo. Essa EDO vai ser:

A indutância, e a resistência, podem ser definidos por constantes ou por funções de . Esse é a função da tensão que passa pelo circuito.

📢 Clique para saber mais:

Circuito RC em Série

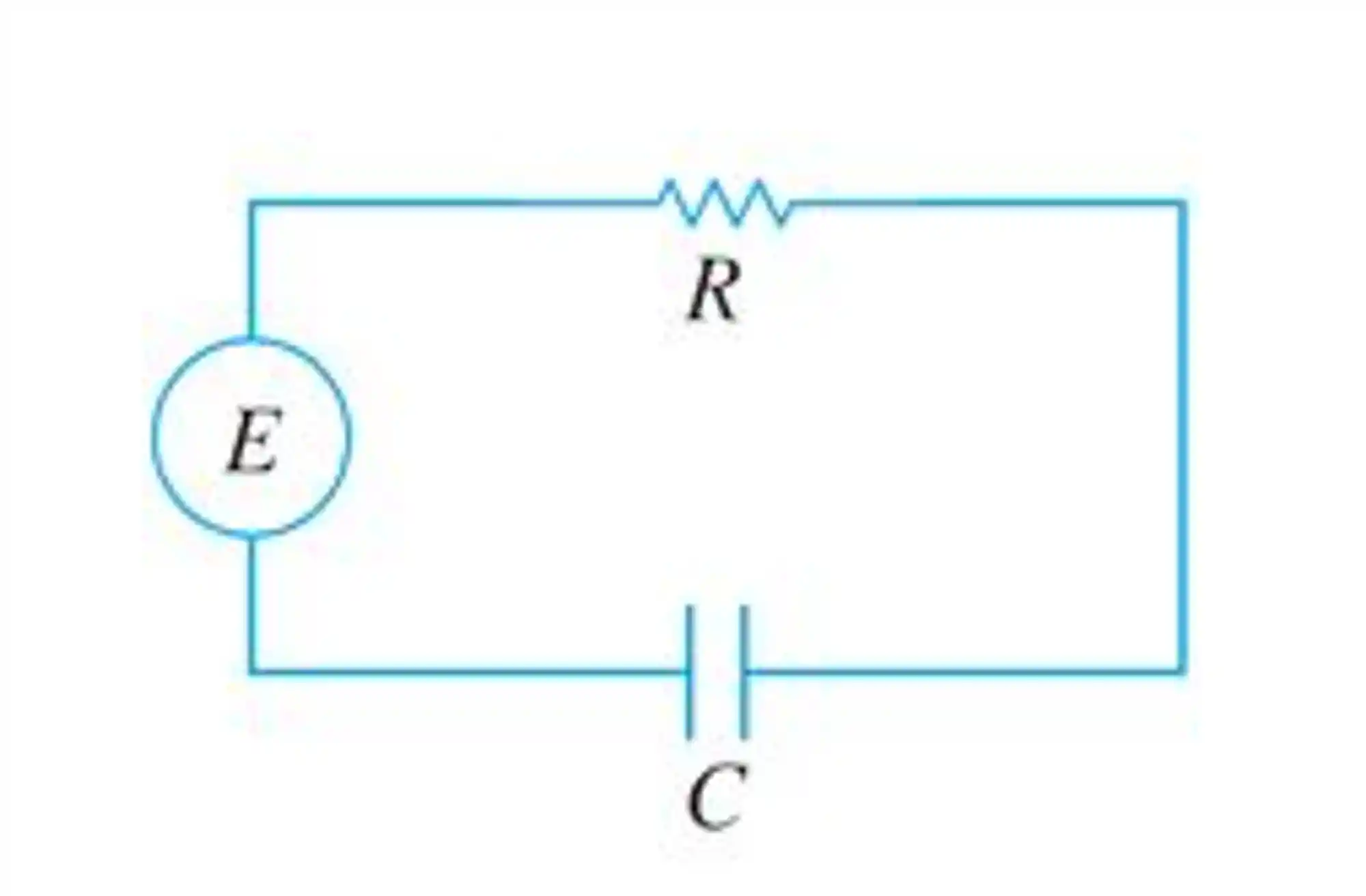
Já o circuito RC é composto por um resistor e um capacitor ligados em série, ele é representado assim:

Aqui vamos ter a EDO para chegar na carga em função do tempo. Essa EDO vai ser:

A capacitância e a resistência podem ser definidos por constantes ou por funções de . Esse E(t) é a função da Tensão que passa pelo circuito. Para resolvermos problemas de circuito elétrico temos que levar essas duas equações no bolso e saber quando aplicá-las!

Quer aprender como usar EDO pra modelar outros sistemas?! Se liga nesse vídeozinho aqui! 👇

Modelagem de um Tanque

É bem comum aparecer um problema de modelagem envolvendo um tanque, fluxos de entrada e saída de volume e concentração de algum produto químico ou coisa semelhante.
Nesse tipo de problema frequentemente serão dados:

  • Fluxo de entrada e saída ;
  • Concentração da entrada;
  • Volume Inicial;
  • Concentração inicial;

O problema vai exigir calcular a quantidade de material no tempo, isso é a função . Para resolver esse tipo de problema, o passo a passo é:

1. Definir as Variáveis

As variáveis de problemas de modelagem envolvendo um tanque costumam ser:

  • a quantidade de produto dissolvido;
  • o volume total do tanque;
  • Fluxo de entrada e fluxo de saída;
  • Concentração de entrada.

2. Determinar as condições Iniciais

Nesse passo a gente verifica as condições das variáveis no tempo zero:

3. Verificar V(t)

  • Se o fluxo de entrada for igual ao fluxo de saída, então . O que é um primeiro sinal para um regime permanente.
  • Mas se o fluxo de entrada for diferente ao fluxo de saída, então:
    • í.

4. Modelar o Problema

í

Onde:

çã
íí

5. Resolver o problema de valor inicial (PVI) para encontrar Q(t)

Nesse último passo é só correr para o abraço!

Modelagem de Forças Resistivas

Usamos equações diferenciais para resolver diversos problemas da física! No caso da utilização de forças resistivas teremos problemas onde existe algo que gera um impedimento a um movimento.
O valor da força de resistência pode variar dependendo da força resistiva definida na questão, mas, normalmente teremos o seguinte formato.

O sinal negativo surge porque a força irá desacelerar o movimento, é uma constante de proporcionalidade e é a velocidade.

Vamos supor um problema literal onde é aplicado em um corpo uma força e ele sofre uma força de resistência . O somatório das forças é igual a força resultante que, por sua vez, é igual o produto entre a massa e a aceleração. Assim:

Chegamos então em uma EDO de primeira ordem! Aqui os valores de , e podem ser constantes, mas também podem ser funções do tempo, isso só vai interferir nas integrais da resolução. Agora vamos praticar com exercícios?!

Modelagem de um Tanque

Modelagem de Forças Resistivas

Exercícios Resolvidos

Exercício Resolvido #1

UERJ, Cálculo 3, Lista 4 do professor Fernando Lopes, Questão 1

Um corpo se move através de um fluido viscoso sob ação de uma força resultante F - K η v , onde K depende da forma do corpo, v é a velocidade do corpo e η é o coeficiente de viscosidade. Obter a velocidade como função do tempo. Suponha que o movimento seja retilíneo, que a força aplicada seja constante e que v 0 = v 0

Passo 1

Po beleza, ele disse que força resultante é: F - K η v , mas sabemos da física que:

∑ F = m a = m d v d t

Assim:

m d v d t = F - K η v

Logo:

m d v d t + K η v = F

Dividindo tudo por m :

d v d t + K η m v = F m

Opa, é uma EDO linear de ordem 1, né não?!

Passo 2

Partiu resolver:

d v d t + K η m v = F m

Comparando lá com a nossa EDO habitual

d v d t + p t v = g ( t )

Vamos ter

p t = K η m

g t = F m

Passo 3

Vou chamar o que a gente chamava de v de I , porque nesse exercício v é a velocidade

Calcular I x = e ∫ p x d x

∫ p t   d t = K η m t

I t = e ∫ p t d t = e K η m t

Passo 4

Agora vamos calcular esse termo aqui

∫ I t ⋅ g t d t

∫ e K η m t ⋅ F m d t = F K η e K η m t

Passo 5

Encontrar a solução:

v t = 1 I t ∫ I t ⋅ g t d t + C

v t = 1 e K η m t F K η e K η m t + C

v t = F K η + C e - K η m t

Passo 6

Agora, vamos substituir o valor inicial que ele nos deu

Então partiu:

v 0 = v 0 = F K η + c e 0 = F K η + c

Daí temos que:

c = v 0 - F K η

Então a resposta fica:

v t = F K η + v 0 - F K η e - K η m t

Resposta

v t = F K η + v 0 - F K η e - K η m t

Exercício Resolvido #2

Exercício nº 7 letra “b” - lista 3 de Cálculo III – IME - UERJ – Prof. Fernando Lopes C. -2014

Resolva o circuito RL:

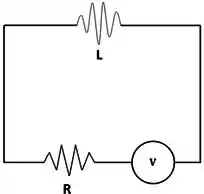
Sabendo que as quedas de voltagem são:

Indutor:   L d I d t Resistor:   I R

E que a força eletromotriz é:

V t = V 0 sen ⁡ w t

E com a lei de Kirchoff: ”A soma algébrica de todas as quedas de tensão em torno de qualquer circuito fechado é nula, ou a tensão aplicada em um circuito fechado é igual à soma das quedas de tensão no resto do circuito.”

Passo 1

Eita que doidera, né não?

Mas a gente viu na teoria que por essa lei de Kirchoff podemos concluir que:

L d I ( t ) d t + I ( t ) R = V ( t )

Mas sabemos que valor da força eletromotriz é: V t = V 0 sen ⁡ w t

Assim:

L d I ( t ) d t + I t R = V 0 sen ⁡ w t

Passo 2

Beleza clã, achamos uma EDO linear de primeira ordem, né? Vamos dividir tudo por L :

d I ( t ) d t + R L I t = V 0 L sen ⁡ w t

p t = R L g t = V 0 L sen ⁡ w t

Passo 3

Calcular a integral ∫ p t d t sem adicionar a constante e ache v t = e ∫ p t d t

∫ p t d t = ∫ R L d t = R L t

Assim ficou :

∫ p t d t = R L t

v t = e ∫ p t d t

v t = e R L t

Passo 4

Calcular a integral ∫ g t ⋅ v ( t ) d t

∫ V 0 L sen ⁡ w t e R L t d t

V 0 L ∫ sen ⁡ ( w t ) e R L t d t

Essa integral pode ser resolvida por duas integrações por partes:

∫ sen ⁡ ( w t ) e R L t d t

Chama de :

w = e R L t → d w = R L e R L t d z = sen ⁡ w t d t → z = - 1 w cos ⁡ w t

Assim:

∫ sen ⁡ ( w t ) e R L t d t = - 1 w e R L t cos ⁡ w t + R w L ∫ cos ⁡ w t e R L t d t

∫ cos ⁡ w t e - R L sen ⁡ t d t = ?

Mesma coisa:

w = e R L t → d w = R L e R L t d z = cos ⁡ w t → z = 1 w sen ⁡ w t

∫ sen ⁡ ( w t ) e R L sen ⁡ t d t = - 1 w e R L t cos ⁡ w t + R w L 1 w e R L t sen ⁡ w t - R w L ∫ sen ⁡ w t e R L t d t

Perceba que a integral que apareceu na esquerda é igual à da direita, então podemos passar ela para o mesmo lado e colocar ela em evidência:

1 + R 2 w 2 L 2 ∫ sen ⁡ ( w t ) e - R L t d t = - 1 w e R L t cos ⁡ w t + R w 2 L e R L t sen ⁡ w t

Assim:

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = - 1 w e R L t cos ⁡ w t 1 + R 2 w 2 L 2 + R w 2 L e R L t sen ⁡ w t 1 + R 2 w 2 L 2

Negócio tá ficando bizarro o.O, mas simbora:

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = - w L 2 e R L t cos ⁡ w t w 2 L 2 + R 2 + R L   e R L t sen ⁡ w t w 2 L 2 + R 2

Negócio tá ficando bizarro o.O, mas simbora:

∫ sen ⁡ ( w t ) e - R L sen ⁡ t d t = e R L t w 2 L 2 + R 2 R L sen ⁡ w t - w L 2 cos ⁡ w t

Então:

V 0 L ⋅ e R L t w 2 L 2 + R 2 ( R L sen ⁡ w t - w L 2 cos ⁡ w t )

Vamos tentar dar uma ajeitada pra ficar com uma aparência melhor:

V 0 e R L t w 2 L 2 + R 2 R sen ⁡ w t - w Lcos ⁡ w t

V 0 e R L t ⋅ w L w 2 L 2 + R 2 R w L sen ⁡ w t - cos ⁡ w t

Passo 5

Então qual é a cara da solução?

I t = 1 v t ∫ g t ⋅ v t d t + C

I ( t ) = V 0 e R L t ⋅ w L w 2 L 2 + R 2 R w L sen ⁡ w t - cos ⁡ w t ⋅ e - R L t + C e - R L t

I ( t ) = V 0 w L w 2 L 2 + R 2 R w L sen ⁡ w t - cos ⁡ w t + C e - R L t

Bem bem, essa já é a resposta do problema, mas para dar a resposta do gabarito um paranauê precisa ser feito. Se a gente usar essa identidade trigonométrica aqui:

a sin ⁡ x + b cos ⁡ x = a 2 + b 2 sen ⁡ x + arctg ⁡ b a

A gente consegue reescrever essa bagaça dessa forma:

R w L sen ⁡ w t - cos ⁡ w t = R 2 w 2 L 2 + - 1 2 sen ⁡ w t - arctg ⁡ w L R

Isso é bastante usado no mundo da vibração, mas por aqui ainda é meio assustador, mas é trigonometria!

R w L sen ⁡ w t - cos ⁡ w t = R 2 + W 2 L 2 w L sen ⁡ w t - arctg ⁡ w L R

Subtituindo:

y = V 0 w L w 2 L 2 + R 2 R 2 + W 2 L 2 w L sen ⁡ w t - arctg ⁡ w L R + C e - R L t

Assim, finalmente:

y = V 0 sen ⁡ w t - arctg ⁡ w L R R 2 + W 2 L 2 + C e - R L t

Uuuuuufaaaaa!!!!

Resposta

y = V 0 sen ⁡ w t - arctg ⁡ w L R R 2 + W 2 L 2 + C e - R L t

Exercício Resolvido #3

UFRJ, Cálculo 2, P1 2009.1, Questão 2

Considere um tanque que possui 1000 litros de água pura. Suponha que ele comece a receber produtos químicos, completamente diluídos em água, a uma taxa de 200 litros por hora, e que a concentração desses produtos na água que ali está entrando varia periodicamente com o tempo t (medido em horas), de acordo com a fórmula

f t = 5 + sen ⁡ t 100 quilogramas por litro

A solução então é misturada completamente e sai do tanque também à taxa de 200 litros por hora. Determine a quantidade de produtos químicos (em quilogramas) que permanece no tanque após t horas.

Lembrete:

∫ e a t sen ⁡ t d t = 1 a 2 + 1 e a t a sen ⁡ t - cos ⁡ t + C ,   C ∈ R   , a ≠ 0

Passo 1

Definições:

Q ( t ) – quantidade (em quilogramas) de produtos químicos no tanque no tempo t

V ( t ) – volume total da solução

fluxo de entrada = 200   l / h

fluxo de saída = 200   l / h

concentração de entrada = f t = 5 + sen ⁡ t 100

Passo 2

Condições iniciais:

V 0 = 1000   l

Q 0 = 0 (água pura inicialmente)

Passo 3

Verificar V ( t ) :

fluxo de entrada = fluxo de saída

Então o volume é constante:

V t = V 0 = 1000

Passo 4

Modelagem:

Q ' t = taxa de entrada - taxa de saída

Calculemos a taxa de entrada:

taxa de entrada = fluxo de entrada ⋅ concentração de entrada

taxa de entrada = ( 200   l / h ) ⋅ 5 + sen ⁡ t 100   kg / l    

⇒ taxa de entrada = 2 5 + sen ⁡ t   kg / h

Calculemos a taxa de saída:

taxa de saída = fluxo de saída ⋅   Q t V t

taxa de saída = ( 200   l / h ) ⋅ Q t 1000   kg / l

⇒ taxa de saída = Q t 5 kg / h

Substituindo na equação:

Q ' t = taxa de entrada - taxa de saída

⇒ Q ' t = 2 5 + sen ⁡ t - Q t 5

⇒ Q ' t + 1 5 Q ( t ) = 2 5 + sen ⁡ t

Logo:

Q ' t + 1 5 Q t = 2 5 + sen ⁡ t Q 0 = 0

Passo 5

Colocar a equação na forma Q ' t + A t ⋅ Q t = B ( t ) :

Já está! Vamos ao próximo passo!

Passo 6

Encontrar A ( t ) e B ( t ) :

Comparando as duas equações:

Q ' t + A t ⋅ Q t = B ( t ) Q ' t + 1 5 ⋅ Q t = 10 + 2 sen ⁡ t

⇒ A t = 1 5 B t = 10 + 2 sen ⁡ t

Passo 7

Calcular a integral ∫ A t   d t sem adicionar a constante:

∫ A t   d t = ∫ 1 5 d t

∫ 1 5 d t = t 5

⇒ ∫ A t   d t = t 5

Passo 8

Calcular fator integrante:

I t = e ∫ A t   d t = e t 5

⇒ I t = e t 5

Passo 9

Calcular a integral ∫ I t ⋅ B t   d t sem adicionar a constante:

∫ I t ⋅ B t d t = ∫ e t 5 ⋅ 10 + 2 sen ⁡ t   d t

∫ e t 5 ( 10 + 2 sen ⁡ t ) d t = 10 ∫ e t 5   d t + 2 ∫ e t 5 sen ⁡ t d t

Calculando a primeira integral:

∫ e t 5   d t = 5 e t 5

Calculando a segunda integral:

∫ e t 5 sen ⁡ t d t

Vamos usar o lembrete que o enunciado forneceu:

∫ e a t sen ⁡ t d t = 1 a 2 + 1 e a t a sen ⁡ t - cos ⁡ t + C

Substituindo a = 1 5 e lembrando que não adicionamos a constante:

⇒ ∫ e 1 5 t sen ⁡ t d t = 1 1 5 2 + 1 e 1 5 t 1 5 sen ⁡ t - cos ⁡ t

⇒ ∫ e 1 5 t sen ⁡ t d t = 1 1 25 + 1 e t 5 1 5 sen ⁡ t - cos ⁡ t

⇒ ∫ e 1 5 t sen ⁡ t d t = 25 26 e t 5 1 5 sen ⁡ t - cos ⁡ t

Ufa! Agora é só substituir a primeira e segunda integral que calculamos:

∫ e t 5 ( 10 + 2 sen ⁡ t ) d t = 10 ∫ e t 5 d t + 2 ∫ e t 5 sen ⁡ t d t

⇒ ∫ e t 5 10 + 2 sen ⁡ t d t = 10 ⋅ 5 e t 5 + 2 ⋅ 25 26 e t 5 1 5 sen ⁡ t - cos ⁡ t

⇒ ∫ e t 5 10 + 2 sen ⁡ t d t = e t 5 50 + 25 13 1 5 sen ⁡ t - cos ⁡ t

Pronto! Então:

∫ I t ⋅ B ( t ) d t = e t 5 50 + 25 13 1 5 sen ⁡ t - cos ⁡ t

Passo 10

Encontrar a solução:

Q t = 1 e t 5 ⋅ e t 5 50 + 25 13 1 5 sen ⁡ t - cos ⁡ t + c

⇒ Q t = 50 + 25 13 1 5 sen ⁡ t - cos ⁡ t + c e - t 5

Passo 11

Encontrar solução particular caso seja um PVI:

Q 0 = 0

Substituindo t = 0 na solução geral:

Q 0 = 50 + 25 13 1 5 sen ⁡ 0 - cos ⁡ 0 + c e - 0 5

⇒ Q 0 = 50 + 25 13 0 - 1 + c ⋅ 1

⇒ Q 0 = 50 - 25 13 + c

Substituindo na condição inicial:

Q 0 = 0

⇒ 50 - 25 13 + c = 0

⇒ c = 25 13 - 50

Fazendo uma continha:

c = 25 - 50 ⋅ 13 13

⇒ c = - 625 13

Substituindo a constante na solução geral:

Q t = 50 + 25 13 1 5 sen ⁡ t - cos ⁡ t - 625 13 e - t 5

⇒ Q t = 50 + 5 13 sen ⁡ t - 25 13 cos ⁡ t - 625 13 e - t 5

Resposta

Q t = 50 + 5 13 sen ⁡ t - 25 13 cos ⁡ t - 625 13 e - t 5

Exercícios de Livros Relacionados

24. Um trenó foguete, com velocidade inicial de 150 milhas/h (≈ 240 km/h), é freado por um canalde água. Suponha que, enquanto está sendo freado, a aceleração a do trenó é dada por a(υ) = –μυ², em que
19. Considere um lago, de volume constante V, contendo, no instante t, uma quantidade Q(t) de poluentes distribuídos uniformemente em todo o lago com uma concentração c(t), onde c(t) = Q(t)/V. Suponha
24. Um trenó foguete, com velocidade inicial de 150 milhas/h (≈ 240 km/h), é freado por um canalde água. Suponha que, enquanto está sendo freado, a aceleração a do trenó é dada por a(υ) = –μυ², em que
6. Suponha que um tanque contendo determinado líquido tem uma saída próxima do fundo. Seja h(t) a altura da superfície do líquido acima da saída no instante t. O princípio de Torricelli2 diz que a vel
6. Suponha que um tanque contendo determinado líquido tem uma saída próxima do fundo. Seja h(t) a altura da superfície do líquido acima da saída no instante t. O princípio de Torricelli2 diz que a vel