Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Aproximação Quadrática de uma Função de Várias Variáveis

Ver Todos os Exercícios

Teoria

Aproximação Quadráticas de uma função

Fala,galera. Já estudamos aproximações lineares para funções de uma variável e de várias variáveis. Mas e se eu não quiser uma aproximação linear, se eu quiser uma aproximação quadrática? Ué, pode isso? Claro que sim! E nós vamos ver como se faz!

Lá em aproximação linear vimos que , para funções de uma variável, nós fazíamos a aproximação pela reta tangente.

Isso faz total sentido se pensarmos que em um ponto bem próximo a reta tangente, o valor dessa reta se confunde com o da própria função. Já para funções de várias variáveis, a aproximação se dava pelo plano tangente.

Mas como eu faço no caso de aproximações quadráticas ??? Bom, no caso de funções de uma variável a aproximação será por uma parábola, enquanto que em funções de várias variáveis ocorre por meio de um paraboloide. Calma que vamos ver passo a passo como se faz isso.

Cálculo: Função de uma variável

Como já adiantamos acima, a aproximação de uma função f x nas proximidades de x = x 0 será feita através de uma parábola y x = a x 2 + b x + c . Graficamente temos:

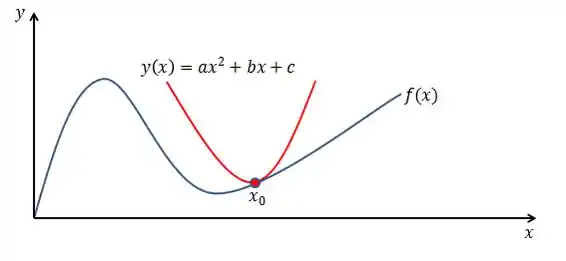
Agora, o nosso trabalho é encontrar os coeficientes dessa parábola. Para que seja uma boa aproximação, a parábola y x deve atender a alguns requisitos:

  • O valor de f x 0 deve ser igual ao da parábola nesse ponto. Ou seja:

    • y x 0 = f x 0

    O que nos leva a:

    a x 0 2 + b x 0 + c = f x 0   i

  • O valor da derivada primeira da função, deve ser igual ao valor da derivada primeira da parábola naquele ponto. Ou seja:

    • y ' x 0 = f ' ( x 0 )

    O que implica em:

    2 a x 0 + b = f ' x 0   i i

  • O valor da derivada segunda da função, deve ser igual ao valor da derivada segunda da parábola naquele ponto. Ou seja:

    • y " x 0 = f " x 0

    O que resulta em:

    2 a = f " x 0   ( i i i )  

    Agora podemos manipular essas equações a fim de encontrar os coeficientes da parábola . Vamos começar por a :

    Da equação i i i temos:

    a = f " x 0 2      

    Vamos encontrar b . Da equação i i temos:

    b = f ' x 0 - 2 a x 0

    Substituindo o valor de a temos:

    b = f ' x 0 - f " x 0 x 0

    Vamos encontrar c . Da equação i temos:

    c = f x 0 - a x 0 2 - b x 0

    Substituindo os valores de a e b temos:

    c = f x 0 - f " x 0 2   x 0 2 - f ' x 0 x 0 + f " x 0 x 0 2  

    Ajeitando:

    c = f x 0 - f ' x 0 x 0 + f " x 0 2   x 0 2

    Beleza! Já temos os coeficientes da parábola, agora é só substituir e encontrar sua equação. Vai ficar assim:

    y x = a x 2 + b x + c

    Substituindo

    y x = f " x 0 2 x 2 + f ' x 0 x - f " x 0 x 0   x + f x 0 - f ' x 0 x 0 + f " x 0 2   x 0 2

    Ajeitando, finalmente temos:

    y x = f x 0 + f ' x 0 x - x 0 + f " x 0 2 x - x 0 2

    Portanto, essa é a equação da parábola que melhor se ajusta a função f x nas proximidades de x = x 0 .

    Cálculo: Função de várias variáveis

    Como já dito, a aproximação quadrática de uma função f x , y nas proximidades de x , y = x 0 , y 0 será feita através do paraboloide z ( x , y ) = a + b x + c y + d x 2 + e y 2 + g x y , Com a , b , c , d , e , g sendo constantes,pois essa equação expressa um paraboloide qualquer.

    Agora, o nosso trabalho é encontrar os coeficientes desse paraboloide. Para que seja uma boa aproximação, o paraboloide z deve atender a alguns requisitos:

  • O valor de f x 0 , y 0 deve ser igual ao do paráboloide nesse ponto. Ou seja:

    • z x 0 , y 0 = f x 0 , y 0

    O que nos leva a:

    a + b x 0 + c y 0 + d x 0 2 + e y 0 2 + g x 0 y 0 = f x 0 , y 0   i v

  • O valor das derivadas primeiras da função, deve ser igual ao valor das derivadas primeiras do paraboloide naquele ponto. Ou seja:

    • z x x 0 , y 0 = f x x 0 , y 0

    z y x 0 , y 0 = f y x 0 , y 0  

    O que implica em:

    b + 2 d x 0 + g y 0 = f x x 0 , y 0   v

    c + 2 e y 0 + g x 0 = f y x 0 , y 0   v i  

  • O valor das derivadas segundas da função, deve ser igual ao valor das derivadas segundas do prabolóide naquele ponto. Ou seja:

z x x x 0 , y 0 = f x x x 0 , y 0  

z x y x 0 , y 0 = f x y x 0 , y 0  

z y y x 0 , y 0 = f y y x 0 , y 0  

z y x x 0 , y 0 = f y x x 0 , y 0  

O que resulta em:

2 d = f x x x 0 , y 0   ( v i i )  

g = f x y x 0 , y 0   v i i i

2 e = f y y x 0 , y 0   i x

g = f y x x 0 , y 0

Obs.: Repare que f y x x 0 , y 0 = f x y x 0 , y 0 = g , portanto toda a análise que será feita a seguir só srve para funções que obedeçam o teorema de Clairaut f x y = f y x .

Agora podemos manipular essas equações a fim de encontrar os coeficientes do parabolóide. Da equação v i i i temos:

g = f x y x 0 , y 0

Da equação i x :

e = f y y x 0 , y 0 2

Da equação ( v i i ) :

d = f x x x 0 , y 0 2

Da equação v :

b = f x x 0 , y 0 - 2 d x 0 - g y 0

b = f x x 0 , y 0 - f x x x 0 , y 0 x 0 - f x y x 0 , y 0 y 0

Da equação v i :

c = f y x 0 , y 0 - 2 e y 0 - g x 0

c = f y x 0 , y 0 - f y y x 0 , y 0 y 0 - f x y x 0 , y 0 x 0

Da equação i v :

a = f x 0 , y 0 - b x 0 - c y 0 - d x 0 2 - e y 0 2 - g x 0 y 0

a = f x 0 , y 0 - ( f x x 0 , y 0 - f x x x 0 , y 0 x 0 - f x y x 0 , y 0 y 0 ) x 0 - f y x 0 , y 0 - f y y x 0 , y 0 y 0 - f x y x 0 , y 0 x 0 y 0 - f x x x 0 , y 0 2 x 0 2 - f y y x 0 , y 0 2 y 0 2 - f x y x 0 , y 0 x 0 y 0

Ajeitando chegamos a:

a = f x 0 , y 0 - f x x 0 , y 0 x 0 - f y x 0 , y 0 y 0 + f x x x 0 , y 0 2 x 0 2 + f y y x 0 , y 0 2 y 0 2 + f x y x 0 , y 0 x 0 + y 0 - x 0 y 0  

Esse ficou grande. Calma que ta acabando. Agora, a ideia é pegar os coeficientes que encontramos e substituir na equação do paraboloide, encontrando assim sua equação.

Então temos:

z = a + b x + c y + d x 2 + e y 2 + g x y

z = f x 0 , y 0 - f x x 0 , y 0 x 0 - f y x 0 , y 0 y 0 + f x x x 0 , y 0 2 x 0 2 + f y y x 0 , y 0 2 y 0 2 + f x y x 0 , y 0 x 0 + y 0 - x 0 y 0 + f x x 0 , y 0 - f x x x 0 , y 0 x 0 - f x y x 0 , y 0 y 0 x + f y x 0 , y 0 - f y y x 0 , y 0 y 0 - f x y x 0 , y 0 x 0 y + f x x x 0 , y 0 2 x 2 + f y y x 0 , y 0 2 y 2 + f x y x 0 , y 0 x y

Ajeitando isso, chegamos a :

z = f x 0 , y 0 + f x x 0 , y 0 x - x 0 + f y x 0 , y 0 y - y 0 + f x x x 0 , y 0 2 x - x 0 2 + f y y x 0 , y 0 2 y - y 0 2 + f x y x 0 , y 0 x - x 0 y - y 0

Portanto, essa é a equação do paraboloide que melhor se ajusta a função f x , y nas proximidades de x , y = x 0 , y 0   .

Vamos ver um exemplo:

Fazer a aproximação quadrática da função f x , y = ln ⁡ x y 2 em x , y = 2,1 .

Sabemos que a equação do paraboloide é dada por

z = f x 0 , y 0 + f x x 0 , y 0 x - x 0 + f y x 0 , y 0 y - y 0 + f x x x 0 , y 0 2 x - x 0 2 + f y y x 0 , y 0 2 y - y 0 2 + f x y x 0 , y 0 x - x 0 y - y 0

Substituindo o ponto dado, a equação fica:

z = f 2,1 + f x 2,1 x - 2 + f y 2,1 y - 1 + f x x 2,1 2 x - 2 2 + f y y 2,1 2 y - 1 2 + f x y 2,1 x - 2 y - 1

Vamos calcular as informações necessárias:

f 2,1 = ln ⁡ 2

As derivadas de primeira ordem são:

f x 2,1 = 1 x y = 1 2

f y 2,1 = 1 x y 2 y = 2 x = 2 2 = 1

As derivadas de segunda ordem são:

f x x 2,1 = - 1 y x 2 = - 1 4

f y y 2,1 = 0

f x y = - 2 x 2 = - 1 2

Substituindo na equação do paraboloide obtemos:

z = ln ⁡ 2 + 1 2 x - 2 + 1 y - 1 - 1 8 x - 2 2 + 0 y - 1 2 - 1 2 x - 2 y - 1

z = ln ⁡ 2 + 1 2 x - 2 + y - 1 - 1 8 x - 2 2 - 1 2 x - 2 y - 1

Bora pros exercícios?!!

Cálculo: Função de várias variáveis

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Aproxime a função f x , y = cos ⁡ x cos ⁡ y por um paraboloide em x , y = 0 , π

Passo 1

Precisamos nos lembrar da equação do paraboloide que melhor se ajusta a f x . Vai ser:

z = f x 0 , y 0 + f x x 0 , y 0 x - x 0 + f y x 0 , y 0 y - y 0 + f x x x 0 , y 0 2 x - x 0 2 + f y y x 0 , y 0 2 y - y 0 2 + f x y x 0 , y 0 x - x 0 y - y 0

Vamos começar expressando a equação em x , y = 0 ,   π . Fica assim:

z = f 0 , π + f x 0 , π x - 0 + f y 0 , π y - π + f x x 0 , π 2 x - 0 2 + f y y 0 , π 2 y - π 2 + f x y 0 , π x - 0 y - π

Podemos ainda calcular:

f 0 , π = cos ⁡ 0 cos ⁡ π = 1 - 1 = - 1

Passo 2

Agora vamos calcular as derivadas de ordem um:

f x 0 , π = - sen ⁡ x cos ⁡ y = - s e n 0 cos ⁡ π = 0

f y 0 , π = - cos ⁡ x s e n y = - cos ⁡ 0 s e n π = 0

Passo 3

Calcularemos as derivadas de segunda ordem:

f x x 0 , π = - cos ⁡ x cos ⁡ y = - cos ⁡ 0 cos ⁡ π = 1

f y y 0 , π = - cos ⁡ x cos ⁡ y = - cos ⁡ 0 cos ⁡ π = 1

f x y 0 , π = s e n x s e n y = s e n 0 s e n π = 0

f y x x , y = s e n x s e n y = s e n 0 s e n π = 0

Passo 4

Substituir as informações na equação do paraboloide:

z = f 0 , π + f x 0 , π x - 0 + f y 0 , π y - π + f x x 0 , π 2 x - 0 2 + f y y 0 , π 2 y - π 2 + f x y 0 , π x - 0 y - π

Substituindo:

z = - 1 + 0 + 0 + 1 2 x 2 + 1 2 y - π 2 + 0

z = - 1 + 1 2 x 2 + 1 2 y - π 2

Resposta

z = - 1 + 1 2 x 2 + 1 2 y - π 2

Exercício Resolvido #2

Elaboração Própria

Utilize a aproximação quadrática para calcular o valor da função f x , y = 4 - 3 x 2 - 2 y 2 no ponto 1.02,0.99

Passo 1

Precisamos nos lembrar da equação do paraboloide que melhor se ajusta a f x . Vai ser:

z = f x 0 , y 0 + f x x 0 , y 0 x - x 0 + f y x 0 , y 0 y - y 0 + f x x x 0 , y 0 2 x - x 0 2 + f y y x 0 , y 0 2 y - y 0 2 + f x y x 0 , y 0 x - x 0 y - y 0

Porém tem um pequeno detalhe, precisamos escolher um ponto próximo ao ponto 1.02,0 . 99 para encontrar o paraboloide que mais se aproxima da função e assim poder calcular f 1.02,0.99

A fim de facilitar as contas, vamos escolher o ponto 1,1 .

Agora, vamos expressar a equação em x , y = 1,1 . Fica assim:

z = f 1 , 1 + f x 1 , 1 x - 1 + f y 1 , 1 y - 1 + f x x 1 , 1 2 x - 1 2 + f y y 1 , 1 2 y - 1 2 + f x y 1 , 1 x - 1 y - 1

Podemos ainda calcular:

f 1 , 1 = 4 - 3 1 2 - 2 1 2 = - 1

Passo 2

Agora vamos calcular as derivadas de ordem um:

f x 1 , 1 = - 6 x = - 6 1 = - 6

f y 1 , 1 = - 4 y = - 4

Passo 3

Calcularemos as derivadas de segunda ordem:

f x x 1 , 1 = - 6

f y y 1 , 1 = - 4

f x y 1 , 1 = 0

f y x x , y = 0

Passo 4

Substituir as informações na equação do paraboloide:

z = f 1,1 + f x 1,1 x - 1 + f y 1,1 y - 1 + f x x 1,1 2 x - 1 2 + f y y 1,1 2 y - 1 2 + f x y 1,1 x - 1 y - 1

Substituindo:

z = - 1 - 6 x - 1 - 4 y - 1 + - 6 2 x - 1 2 + - 4 2 y - 1 2 + 0 x - 1 y - 1

z = - 1 - 6 x - 1 - 4 y - 1 - 3 x - 1 2 - 2 y - 1 2

Passo 5

Agora só falta calcular z 1.02,0 . 99

Temos:

z = - 1 - 6 1.02 - 1 - 4 0.99 - 1 - 3 1.02 - 1 2 - 2 0.99 - 1 2

z = - 1,0814

Resposta

z = - 1,0814

Exercícios de Livros Relacionados

Nos Exercícios 1-10, utilize a fórmula de Taylor para ƒ(x, y) na origem para encontrar aproximações quadráticas e cúbicas de ƒ próximas à origem. f ( x , y ) = s e n ⁡ x c o s ⁡ y
Utilize a fórmula de Taylor para encontrar uma aproximaçãoquadrática de ƒ(x, y) = cos x cos y na origem. Calcule o erro naaproximação se |x| ≤ 0,1 e |y| ≤ 0,1
Nos Exercícios 1-10, utilize a fórmula de Taylor para ƒ(x, y) na origem para encontrar aproximações quadráticas e cúbicas de ƒ próximas à origem. f ( x , y ) = l n ⁡ ( 2 x + y + 1 )
Nos Exercícios 1-10, utilize a fórmula de Taylor para ƒ(x, y) na origem para encontrar aproximações quadráticas e cúbicas de ƒ próximas à origem.ƒ(x, y) = xey
Nos Exercícios 1-10, utilize a fórmula de Taylor para ƒ(x, y) na origem para encontrar aproximações quadráticas e cúbicas de ƒ próximas à origem. f ( x , y ) = e x c o s ⁡ y