Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integrais De Linha - Campo Escalar

Ver Todos os Exercícios

Teoria

Fala aí, nós somos o Responde Aí, a maior plataforma de exatas do Brasil, que vai salvar o seu semestre!!

Nosso papo aqui hoje é sobre as integrais de linha em um campo escalar. Se você chegou até essa página é porque precisa aprender esse conteúdo e nós vamos te ajudar nisso.

Conhecimentos Prévios

Bom, antes de você embarcar nessa aventura das integrais de linha de um campo escalar é interessante você já ter alguns conhecimentos adquiridos. Eu vou eles deixar aqui embaixo listados👇🏾

✅ Parametrização de Curvas

O que é uma Integral de Linha

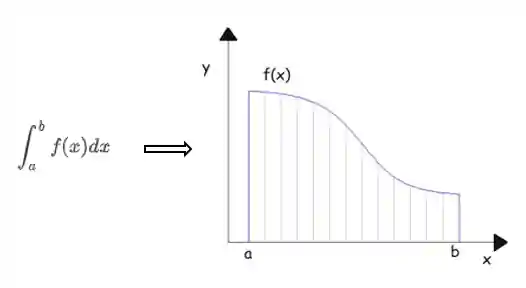
O conceito de integral de linha é bem semelhante com o de integral simples. Nas integrais simples a gente tem uma função e integramos ela dentro de um intervalo e essa integral nos dá a área abaixo da função nesse intervalo. Desse jeitinho aqui:

Agora, na integral de linha, a gente quer integrar uma função, mas não em intervalo de e sim em uma curva do plano . Nesse caso, nós temos que o nosso intervalo de integração é uma curva, que varia tanto com quanto com , então a nossa função integrando será do tipo , sacou?

A integral de linha pode ser interpretada como a área entre a curva, que chamamos de e a função, como nessa figura aqui:

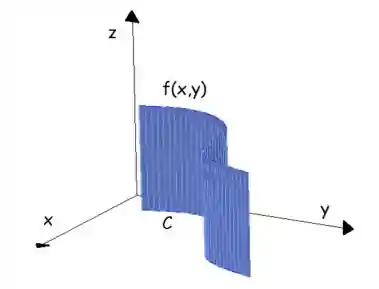
Nós representamos a integral de linha dessa maneira aqui:

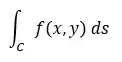
Onde é o que chamamos de infinitesimal da curva, assim como tínhamos o na integral simples.

Como calcular uma Integral de Linha?

Essa é a parte importante e que todo mundo quer saber, né? hahaha

Acho que a coisa mais estranha que aparece na integral de linha é aquele , mas vou te convencer que não tem nenhum mistério.

Para entendermos como calcula, vamos pegar um exemplo. Suponha que a nossa função seja e que a curva seja um círculo de raio e centro na origem.

A primeira coisa que devemos fazer para resolver essa integral é parametrizar a curva. Esse círculo é parametrizado da seguinte forma:

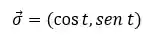
Com o variando de à : .

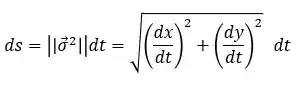
Depois de parametrizar a curva você vai usar a seguinte fórmula para encontrar o :

QUE? Entendeu nada, né? hahaha Calma, vamos aplicar no nosso exemplo. Vamos olhar a parametrização que fizemos da curva e definir quem é e quem é :

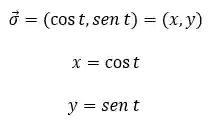
Agora, vamos derivar e em relação a :

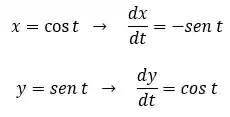
Agora, a gente coloca essa informação na fórmula para :

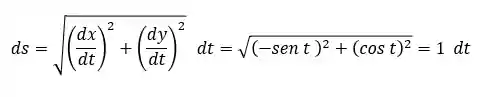
E esse é o nosso .

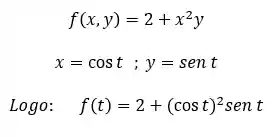
Após definir o , o nosso próximo passo é escrever a função em termos de somente. Lembra que lá na parametrização da curva nós definimos quem era o e quem era o ?, Então, agora a gente vai pegar esse valor de e em função de e vamos substituir na função, assim:

Agora, está tudo pronto para montar a nossa integral de linha:

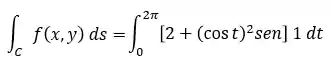
Só para deixar tudo bem explicadinho: os limites de integração vieram dos valores de lá da parametrização. O termo que está no primeiro parêntese é a em termos de e em seguida temos o que a gente calculou.

Agora é só resolver como uma integral simples:

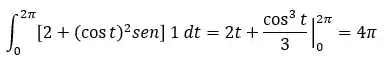
Viu?! Não é tão complicado assim.

Resumo

Vamos fazer aqui um passo a passo para calcular a integral de linha:

PASSO 1: Montar o problema

PASSO 2: Parametrizar a curva

PASSO 3: Calcular o

PASSO 4: Escrever em função de

PASSO 5: Substituir e em função de na integral

PASSO 6: Calcular a integral

Agora vem a hora de praticar e fixar esse conteúdo que aprendemos. Vou deixar em seguida um exercício sobre integrais de linha em campo escalar em vídeo, onde nós do Responde Aí resolvemos o exercício passo a passo junto com você 👇🏾

Exercício (Vídeo)

Curtiu nosso conteúdo? Então assina com a gente para ter acesso a muito mais e mandar super bem no semestre!! 😉

Como calcular uma Integral de Linha?

Resumo

Exercícios Resolvidos

Exercício Resolvido #1

USP - Cálculo 3 - P1 2015 – 2b

Seja C a curva cujo traço é a parte da elipse x 2 3 + y 2 4 = 1 no primeiro quadrante.

Calcule a massa de C, sendo a densidade δ x , y = x y .

Passo 1

Na teoria, a gente viu que a massa de uma curva é dada pela integral de linha:

∫ C δ x , y d s

A densidade a gente já tem, δ x , y = x y . Então, fica só faltando parametrizar a curva e calcular σ → ' t   d t . Vamos lá!

Passo 2

O enunciado nos deu a equação da elipse da seguinte forma:

x 2 3 + y 2 4 = 1

Pra poder parametrizar isso, vamos precisar usar a relação fundamental trigonométrica que diz isso aqui

cos 2 ⁡ t + sen 2 ⁡ t = 1

Portanto

x 2 3 = cos 2 ⁡ t

x 2 = 3 cos 2 ⁡ t

x = 3 cos ⁡ t

Agora o mesmo para y

y 2 4 = sen 2 ⁡ t

y 2 = 4 sen 2 ⁡ t

y = 2 sen ⁡ t

Ele tem parametrização:

σ → = 3 cos ⁡ t ,   2 sen ⁡ t

Mas como só temos o pedaço do primeiro quadrante:

0 ≤ t ≤ π 2

Passo 3

Vamos lembrar a fórmula de σ → ' t d t :

σ → ' t d t =   d x d t 2 + d y d t 2 d t

Precisamos colocar as derivas da parametrização dentro da raiz, certo? Vamos calcular elas aqui rapidinho então

x t = 3 cos ⁡ t → x ' t = - 3 sen ⁡ t

y t = 2 sen ⁡ t → y ' t = 2 cos ⁡ t

σ → ' = - 3 sen ⁡ t 2 + 2 cos ⁡ t 2

= 3 sen 2 ⁡ t + 4 cos 2 ⁡ t

= 3 sen 2 ⁡ t + 3 cos 2 ⁡ t + cos 2 ⁡ t

= 3 sen 2 ⁡ t + cos 2 ⁡ t + cos 2 ⁡ t = cos 2 ⁡ t + 3

E agora é só jogar na integral!

Passo 4

Voltando lá, o que a gente queria calcular era:

∫ a b δ x t , y t ∙ σ → ' t   d t = ∫ 0 π 2 3 cos ⁡ t ∙   2 sen ⁡ t   ∙ cos 2 ⁡ t + 3   d t

Que parece meio estranho de calcular, mas podemos resolver fazendo a substituição:

u = cos 2 ⁡ t + 3

d u = 2 cos ⁡ t ∙ - sen ⁡ t   d t → d t = d u - 2 cos ⁡ t ∙ sen ⁡ t

Então vamos ter:

∫ 3 cos ⁡ t ∙   2 sen ⁡ t   ∙ cos 2 ⁡ t + 3   d t = ∫ - 3 ∙ u   d u

= - 3 ∙ 2 u 3 2 3 = - 3 ∙ 2 3 ∙ cos 2 ⁡ t + 3 3 2

E aplicando os limites de integração, temos:

2 3 3 ∙ - cos 2 ⁡ t + 3 3 2 │ 0 π 2 = 3 ∙ 2 3 ∙ - 3 3 2 + 4 3 2

= - 18 + 2 3 ∙ 8 3 = 16 3 - 18 3

Resposta

16 3 - 18 3

Exercício Resolvido #2

UFF - Cálculo IIIA - Lista 3, GMA 2015.2 – 14

Um pintor deseja pintar os dois lados de uma cerca cuja base é uma curva C no plano x y dada por x 2 / 3 + y 2 / 3 = 20 2 / 3 , para x ≥ 0 e y ≥ 0 . A altura em cada ponto x , y ∈ C é dada por f x , y = y . Se o pintor cobra R reais por m 2 , quanto ele receberá?

Passo 1

Lembra que a integral de linha é a área embaixo da curva, onde a altura é dada por f x , y ?

Então, essa área vai ser exatamente a área da cerca. E o que ele pede na verdade é:

∫ C f x , y d s

Onde f x , y = y e C é a curva x 2 / 3 + y 2 / 3 = 20 2 / 3 , para x ≥ 0 e y ≥ 0 .

Passo 2

Vamos começar achando a parametrização dessa curva. Se ela não tivesse aquele sobre 3 no expoente, poderíamos fazer uma substituição de circunferência.

x 2 / 3 + y 2 / 3 = 20 2 / 3

x 1 / 3 2 + y 1 / 3 2 = 20 1 / 3 2

x 1 / 3 20 1 / 3 2 + y 1 / 3 20 1 / 3 2 = 1

Então, vamos fazer algo parecido, olhando pra essa equação como a relação trigonométrica

cos 2 ⁡ t + sen 2 ⁡ t = 1

Temos que

x 1 / 3 20 1 / 3 = cos ⁡ t ⇒ x 20 = cos 3 ⁡ t

x = 20 cos 3 ⁡ t

y 1 / 3 20 1 / 3 = sen ⁡ t ⇒ y 20 = sen 3 ⁡ t

y = 20 sen 3 ⁡ t

Pronto temos a nossa parametrização

σ → ( t ) = 20 cos 3 ⁡ t , 20 sen 3 ⁡ t

Ele diz que pegou a parte positiva de x e y , então, vamos ter

cos ⁡ t > 0   e sen ⁡ t > 0 ∴ t ∈ 0 ; π 2

Passo 3

Vamos calcular as derivadas da parametrização

d x d t = - 60 cos 2 ⁡ t sen ⁡ t

d y d t = 60 sen 2 ⁡ t cos ⁡ t

Então, calculamos σ t → ' :

σ t → ' = - 60 cos 2 ⁡ t sen ⁡ t 2 + 60 sen 2 ⁡ t cos ⁡ t 2 = 60 cos 4 ⁡ t sen 2 ⁡ t + sen 4 ⁡ t cos 2 ⁡ t

⇒ 60 cos 2 ⁡ t sen 2 ⁡ t cos 2 ⁡ t + sen 2 ⁡ t = 60 cos 2 ⁡ t sen 2 ⁡ t = 60 | cos ⁡ t sen ⁡ t |

Como o enunciado pede cos ⁡ t > 0 e sen ⁡ t > 0 , podemos tirar o módulo e ficar com

60 cos ⁡ t sen ⁡ t

Passo 4

Substituindo na integral

∫ 0 π / 2 20 sen 3 ⁡ t .   60 cos ⁡ t sen ⁡ t d t = 1200 ∫ 0 π / 2 sen 4 ⁡ t cos ⁡ t d t

Vamos achar a integral ignorando os limites de integração

∫ sen 4 ⁡ t cos ⁡ t d t

Fazendo

u = sen ⁡ t

d u = cos ⁡ t d t

Substituindo vamos ter

∫ sen 4 ⁡ t cos ⁡ t d t = ∫ u 4 d u = u 5 5

Desubstituindo

u 5 5 = sen 5 ⁡ t 5

1200 ∫ 0 π / 2 sen 4 ⁡ t cos ⁡ t d t = 1200 sen 5 ⁡ t 5 t = 0 π / 2 = 1200 1 5 = 240

Passo 5

A cerca tem em cada lado uma área de 240 , então a área total que ele vai pintar vai ser

A = 2.240 = 480

O valor gasto vai ser isso vezes R

480 R

Resposta

480 R

Exercício Resolvido #3

UFRJ, Cálculo III, P1-2012.2, 3

Calcule a integral de linha da função escalar f x , y = | x | ao longo da curva C parametrizada por

σ : 0 ,   π / 2 → R 2 ,   t → ( e t cos ⁡ t , e t sen ⁡ t )

Passo 1

A integral de linha vai ser representada assim: ∫ C   | x | d s

Temos que a = 0 e b = π / 2 pelo próprio enunciado. A parametrização da curva nos dá x t = e t cos ⁡ t e y t = e t sen ⁡ t .

Passo 2

Começaremos calculando σ → ' = d e t cos ⁡ t d t , d e t sen ⁡ t d t =

= e t cos ⁡ t - e t sen ⁡ t , e t sen ⁡ t + e t cos ⁡ t =

= e t cos ⁡ t - sen ⁡ t , sen ⁡ t + cos ⁡ t

Passo 3

Agora, calculamos σ → ' :

σ → ' = e 2 t cos ⁡ t - sen ⁡ t 2 + e 2 t sen ⁡ t + cos ⁡ t 2 =

= e t cos 2 ⁡ t - 2 cos ⁡ t sen ⁡ t + sen 2 ⁡ t + sen 2 ⁡ t + 2 cos ⁡ t sen ⁡ t + cos 2 ⁡ t =

= e t 2

Passo 4

Podemos, então, substituir σ → ' na integral, escrevendo   | x | em função de t :

∫ 0 π / 2 | e t cos ⁡ t | . e t 2 d t =

= 2 ∫ 0 π / 2 e 2 t cos ⁡ t d t =

Passo 5

Vamos, agora, integrar por partes, chamando e 2 t = u e cos ⁡ t = v ' . Temos 2 e 2 t = u ' e sen ⁡ t = v .

∫ u v ' = u v - ∫ u ' v

∫ e 2 t cos ⁡ t d t = e 2 t sen ⁡ t - 2 ∫ e 2 t sen ⁡ t   d t

Chamando, agora, e 2 t = u e sen ⁡ t = v ' , temos u ' = 2 e 2 t e v = - cos ⁡ t e a integral passa a ser:

∫ e 2 t cos ⁡ t d t = e 2 t sen ⁡ t - 2 - e 2 t cos ⁡ t + 2 ∫ e 2 t cos ⁡ t d t

∫ e 2 t cos ⁡ t d t = e 2 t sen ⁡ t + 2 e 2 t cos ⁡ t - 4 ∫ e 2 t cos ⁡ t d t =

∫ e 2 t cos ⁡ t d t = e 2 t ( sen ⁡ t + 2 cos ⁡ t ) 5

Substituindo na integral inicial, temos:

2 ∫ 0 π 2 e 2 t cos ⁡ t d t = 2 5   e 2 t ( sen ⁡ t + 2 cos ⁡ t ) 0 π 2 =

= 2 5 e π 1 + 0 - 1 ( 0 + 2 ) =

Resposta

2 5 e π - 2

Exercícios de Livros Relacionados

Calcule a integral de linha, onde C é a curva dada. ∫ C x + 2 y d x + x 2 d y C consiste nos segmentos de reta de ( 0,0 ) a ( 2,1 ) e de ( 2,1 ) a ( 3,0 ) .
Calcule o valor da integral de linha, onde C é a metade é a metade do círculo x 2 + y 2 = 16
Calcule a integral de linha, onde C é a curva dada.int_C x y^3 d s , C : x = 4 s e n t , y = 4 cos t , z = 3 t , 0 = t = (pi)/(2)
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = c o s 3 t , y = s e n 3 t no primeiro quadrante.
Calcule a integral de linha, onde C é a curva dada.int_C x y^4 d s , C é a m e t a d e d i r e i t a d o c í r c u l o x^2 + y^2 = 16 é í