Parametrização de Curvas
Produzido por Arthur Melo de AlmeidaTeoria
Bem vindo ao RespondeAí! Agora aperta o cinto e vem comigo porque você vai aprender, de uma vez por todas a fazer Parametrização de Curvas e arrasar nas suas provas!
Essa matéria é muito importante para Integrais de Linha, então vem comigo que quando você chegar lá você vai estar fera!
Beleza, mas o que é parametrizar uma curva?
Parametrização de curvas é descrever uma função apenas com uma variável!
Vamos pegar a curva :
E vamos transforma-la em uma equação paramétrica!
Essa função é descrita a partir de duas variáveis
Então isso quer dizer que:
Então podemos escrever a curva parametrizada, que é igual a:
Esse caso é chamado de parametrização explícita, afinal o
Bom, então temos que, a parametrização nada mais é do que definir os valores de ,
É válido informar aqui que toda curva tem infinitas formas de ser parametrizada! Ou seja, o gabarito sempre vai conter uma possibilidade de parametrização, geralmente a mais comum, mas se a que você criou também representa a mesma curva, sua resposta vai estar certa também!
Por exemplo:
Essas duas parametrizações representam a mesma reta
Curvas Clássicas:
Vamos dar uma olhada agora nas parametrizações mais clássicas: retas, circunferências, elipses hipérboles. Sabendo elas, seremos capazes de fazer a maioria dos nossos exercícios!
Retas:
Imagine que temos uma reta que passe pelo ponto
Generalizando: Podemos parametrizar qualquer reta sabendo o seu vetor direção
Chegamos então na seguinte equação paramétrica:
Com:
Os limites da reta são infinitos, felizmente quase nunca trabalhamos com retas mas sim segmentos delas, ou seja, vamos ter limites
Circunferência/Elipse:
Imagina que você tenha que parametrizar essa elipse aqui:
Ficaríamos com a seguinte parametrização:
Generalizando: A elipse é dada pela seguinte equação
Ela vai ser parametrizada pela relação fundamental trigonométrica
A circunferência vai ser o caso em que
Sua parametrização, pelo mesmo motivo, é dada por:
Agora vamos para um exemplo de como parametrizar uma circunferência
Podemos escrever:
Perceba que, para cada valor de
Graficamente temos:
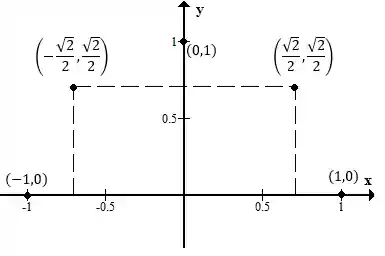
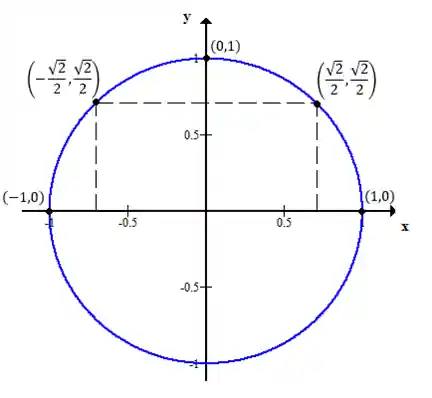
Dessa forma, se juntarmos todos os pontos de a formamos a curva inteira inicial.
Hipérbole:
A forma geral da hipérbole é dada pela seguinte equação:
Ela vai ser parametrizada pela relação fundamental trigonométrica (como se todo mundo lembrasse dessa porcaria né).
Então o ramo da hipérbole situado em
E o ramo situado em
Vale lembrar que o
Dessa forma, se juntarmos todos os pontos de a formamos a curva inteira inicial.
Interseção de Superfícies
Essa revisão trouxe as curvas básicas do cálculo, infelizmente, em alguns casos, nossas curvas vão ser um pouco mais difíceis que essas. Alguns exercícios vão pedir pra gente parametrizar interseções de superfícies, nesses casos vamos precisar escolher a estratégia correta para parametrizar a curva.
Lembre-se sempre do princípio básico da parametrização: Precisamos escrever
Exemplo: Encontre uma parametrização da curva
Primeiramente vamos fazer um esboço dessas superfícies pra ter uma noção da curva que queremos parametrizar.
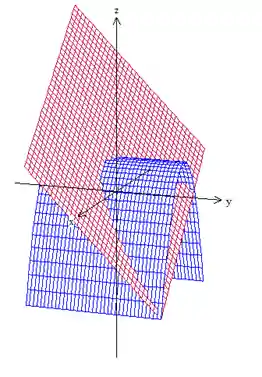
A curva de interseção dessas duas superfícies é essa aqui:
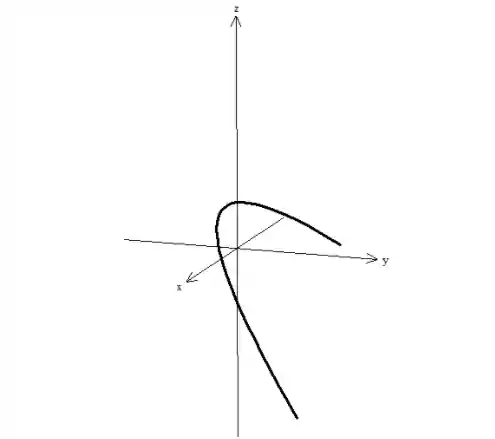
Agora que esboçamos a curva, precisamos analisar as equações do enunciado e, de alguma forma, sumir com as variáveis, deixando tudo em função de apenas uma. Isso muda de exercício para exercício, por isso recomendo que treine bastante isso aqui com exercícios resolvidos, com o tempo a gente começa a perceber semelhanças entre eles!
As equações do nosso exemplo são:
Perceba que
Mas sabemos que
Pronto, parametrizamos a curva! Falta só um detalhe, o enunciado diz também que somente quer o pedaço entre
Para fazer isso, precisamos partir de alguma das nossas varáveis já parametrizadas e que sabemos seu valor no começo e no fim do intervalo. Nesse caso, nos pontos que o enunciado deu,
Agora sim está tudo pronto:
Pra finalizar, vai aqui outro detalhe importante das curvas, sempre que definimos os limites do parâmetro, definimos também uma orientação da curva, ou seja, quando dizemos que , necessariamente nossa reta tem esse sentido geométrico:
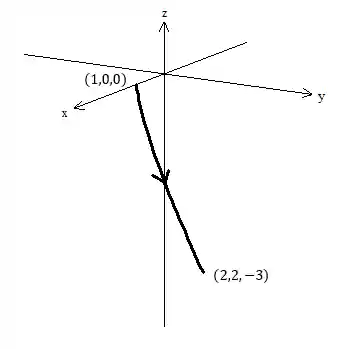
Se quisermos outro sentido, precisamos parametrizar de outra forma! Por exemplo, o sentido inverso dessa curva seria parametrizado por:
Tome muito cuidado com a orientação da sua curva! Pode parecer só um sinal de menos, mas muda bastante coisa e pode tirar ponto na sua prova.
Vamos agora partir pros exercícios pra fixar bem essa ideia na cabeça! Vamos lá?
Curvas Clássicas:
Interseção de Superfícies
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009 – Modificado
Parametrize a curva , fronteira do triângulo de vértices , e , orientada no sentido anti-horário.
Dica: Aqui é preciso parametrizar cada um dos lados do triângulo de forma independente, afinal, cada um deles é um segmento de uma reta diferente.
Passo 1
Como já diz a nossa dica, vamos precisar descobrir a equação de cada uma das retas pra poder parametrizar a curva inteira.
Lembrando que a parametrização nada mais é do que definir os valores de de forma independente e em função de um único parâmetro (pode chamar de uma variável também, é o mesmo significado de parâmetro)
Antes de mais nada, vamos esboçar esse triângulo
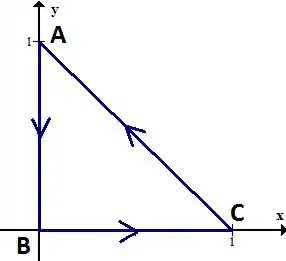
Beleza, precisamos então, para cada um dos lados do triângulo, encontrar o vetor direção e depois parametrizar o segmento de reta tomando cuidado com o sentido que escolhemos.
Tendo o vetor direção , onde e indicam a direção do vetor, e sabendo o ponto inicial , sabemos que a parametrização do segmente vai ser
Depois escolhemos ou para determinar os limites de , vamos lá?
Passo 2
Vamos começar pela reta que se encontra no eixo , vamos chama-la de . Ela é o segmento de reta que liga a , certo? Seu vetor direção
É importante lembrar que , que seria o vetor no outro sentido, tome cuidado com isso!
Beleza, nessa reta aqui, já temos dois pontos e , podemos escolher qualquer um deles como , o que vai mudar vão ser os limites de . Aqui vou fazer os dois casos só pra você ver como fica, nas próximas retas vamos sempre escolher apenas um.
Para o ponto a parametrização fica
Ué? pode ser igual a zero?! Pode sim! O que isso quer dizer é que, para qualquer valor de , a coordenada da reta vai sempre ser zero. Se você olhar pro esboço dá pra perceber que isso é verdade.
E quais os limites de nesse caso? Vamos ver isso por , que vai de a
E se escolhêssemos o outro ponto dessa reta pra fazer a parametrização? Olha só como fica!
Sendo que vai de a também, com isso
Ambas parametrizações estão corretas!
Passo 3
Vamos para o próximo seguimento de reta, chamaremos de que liga a . Para encontramos o vetor direção é só fazer o ponto final menos o inicial, certo?
Escolhendo o ponto para parametrizar essa reta ficamos com
De novo um termo é igual a zero e, de novo, isso não é problema! Veja que realmente sempre é zero nessa reta, tranquilo? Vamos ver os limites de agora.
Sabemos que vai de até , portanto
Passo 4
Vamos para o último segmento de reta , aquele que liga a . Novamente vamos encontrar o vetor direção pela diferença entre os pontos final e inicial
Escolhendo o ponto para parametrizar a reta, ficamos com
Para determinar os limites de , sabemos que começa valendo zero no ponto e termina valendo no ponto , portanto
Veja que, pela parametrização de
Portanto, de fato essa parametrização leva até .
Passo 5
Pronto! Agora só juntando tudo pra ficar bonito
Onde
Resposta
Exercício Resolvido #2
Elaboração Própria
Encontre a parametrização da curva dada equação
Respeitando a inequação
Passo 1
Vamos lá galera, essa curva aí é uma daquelas clássicas dada na teoria, lembra? Quando falamos de elipse e circunferência sempre temos e se somando, essa fórmula aqui
Nesse nosso caso não está igual a , né? Mas isso não é problema, é só dividir por dos dois lados, fica assim
O esboço é esse aqui
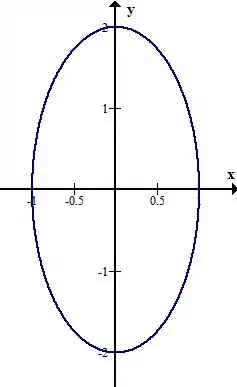
Passo 2
Pra parametrizar isso aí a gente usa a relação fundamental da trigonometria
Passo 3
Teoricamente essa seria a nossa resposta, só que a questão bota uma outra limitação ali, ela diz que
Ué, mas o que isso quer dizer? Pensa o seguinte, na elipse completa os limites de e são
Existem pontos em que o produto de por não dá positivo (maior que zero). Po, então como podemos garantir que de fato é positivo?
Bom, vamos ter que fazer um estudo de sinal aqui, pensa só, quando é positivo e é positivo, o produto também vai ser positivo! Agora, quando um é positivo e o outro negativo, o produto dá negativo. De forma geral é isso aqui
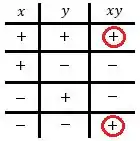
Então, para que , precisamos que e sejam positivos ou que ambos sejam negativos. E quando isso acontece? O plano é dividido em quatro quadrantes, vamos analisar cada um deles separadamente aqui
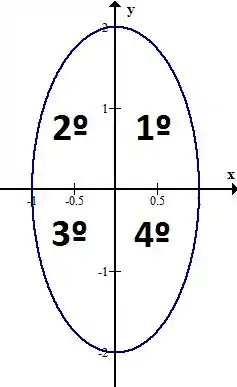
No 1º quadrante temos que , nessa região e são positivos, então o produto também é maior que zero
No 2º quadrante temos que , aqui é negativo e é positivo, então o produto é menor que zero
No 3º quadrante temos que , nessa região e são negativos, então o produto é maior que zero
No 4º quadrante temos que , nessa região é positivo e é negativo, então o produto é menor que zero
Portanto, somente no primeiro e no terceiro quadrante temos , portanto os limites de são
Resposta
Exercício Resolvido #3
Elaboração Própria
Parametrize a curva dada pela interseção do cilindro com o plano
Passo 1
Bom, galera, interseção de superfícies aqui, né? Vamos esboçar tudo aqui antes de mais nada pra visualizar melhor a questão
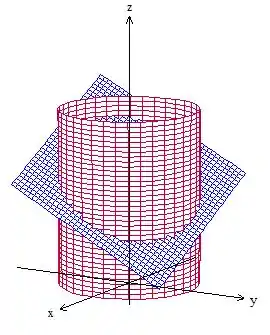
A curva é essa aqui
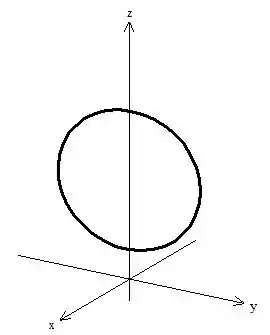
Para parametrizar isso vamos ter que analisar as equações das superfícies
Passo 2
Vamos analisar essa primeira equação do cilindro ali de cima, podemos parametrizar pela equação fundamental da trigonometria
Bem simples até, né? Foi porque escolhemos essa equação, que é uma daquelas clássicas, primeiro! Sempre comece pela equação que é fácil de ser parametrizada, beleza?
Passo 3
Vamos continuar aqui então. Já temos e parametrizados, certo? Conseguimos encontrar os parâmetros de pela equação do plano!
Substituindo os valores de e
E pronto, agora só pra organizar, nossa curva pode ser escrita de uma forma única como
Resposta
Exercício Resolvido #4
Elaboração Própria
Parametrize a curva dada pela interseção das superfícies
Passo 1
Vamos começar com um esboço dessas superfícies que são um pouco diferentes, né?
A primeira é uma esfera de raio , dada pela equação
A segunda é a parte superior de um cone deslocado no eixo , dada pela equação
Desenhando fica muito mais fácil de entender, olha só:
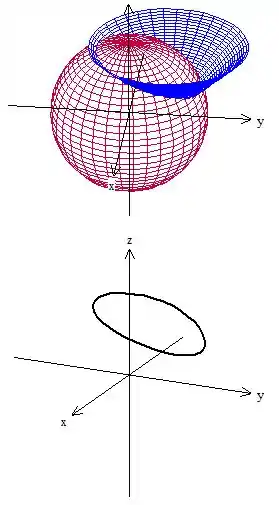
Bom, agora precisamos só analisar as equações e encontrar alguma forma de escrever todas as nossas variáveis em função de um único parâmetro. As equações são essas aqui
Passo 2
Nesse exercício aqui a gente não tem nenhuma equação facilmente parametrizada direto, né? Vamos ter que tentar juntar as duas retirando alguma variável. Ué, como assim? Dá uma olhada aqui, vou mexer um pouco nessa segunda equação
Agora vamos substituir esse na primeira equação lá da esfera!
Passo 3
Po, mas assim a gente não consegue visualizar absolutamente nada! Vamos reorganizar essa equação tentando encontrar aquela relação fundamental, lembra? Essa aqui
Vamos lá então
Po, pra transformas esse termo em algo do tipo , vamos descobrir quem vai ser esse , então
Deste modo,
Reescrevendo a equação lá em cima
Quase tudo pronto, agora só falta deixar o termo ali na direita, fica assim
Passo 4
Agora podemos igualar isso à relação , com isso
Agora para achar a parametrização de
Passo 5
Pronto, já temos e , agora é só substituir em alguma equação pra achar . A segunda já temos isolado, vamos substituir lá mesmo
Vamos fazer produto notável desse
Lembrando que . Então ali, a gente só colocou o em evidência. Seguindo,
Ufa! Terminamos! Pra finalizar vamos colocar tudo junto
Resposta
Exercício Resolvido #5
USP - Cálculo 2 - P1 2012 - 2b – Modificado
Seja a superfície de equação . Encontre uma parametrização para a intersecção de com o plano .
Passo 1
Essa superfície é bem difícil de esboçar, galera, se você não conseguiu não tem problema. A gente vai te mostrar aqui como ela é, mas você pode fazer a questão sem esse esboço. A superfície é essa aqui
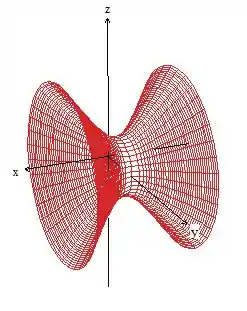
Precisamos da interseção dessa curva com o plano , o esboço é esse
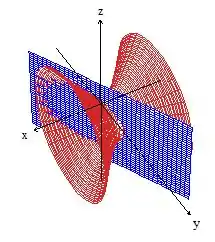
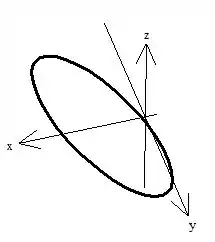
Vamos precisar analisar as duas equações pra dar um jeito de escrever tudo em função de um parâmetro só, vamos lá?
Passo 2
As equações são essas aqui
Vamos tentar isolar algum termo na segunda e substituir na primeira pra ver como fica
Tendo isolado, agora vamos substituir na primeira equação
Precisamos transformar esse termo em algo da forma
Voltando pra equação
Não podemos parametrizar ainda com a equação dessa forma, precisamos deixar o termo do lado direito da equação! Não tem problema, só dividir por nos dois lados
Passo 3
Tendo a equação dessa forma, para parametrizar é só relacionar isso com a equação fundamental que diz
Passo 4
Pronto, agora que temos a parametrização de e fica fácil achar a de , só procurar alguma equação mais fácil e substituir. A equação do plano parece mais simples, né?
Passo 5
Pronto! Só resumindo tudo aqui na resposta e ficamos com a seguinte parametrização