Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Todos os Exercícios

Teoria

O momento de inércia (ou segundo momento) de uma partícula em relação a um eixo é definido como m r 2 , onde m é a massa da partícula e r é a distância entre esse eixo e a partícula.

Se quisermos calcular o momento de inércia com relação ao eixo x da placa D com densidade δ ( x , y ) , teremos que a distância r coincide com a coordenada y . Assim,

I x = ∬ D   y 2   d m = ∬ D   y 2   δ ( x , y ) d A

Para o momento de inércia em relação a y , temos o contrário: a distância é x

I y = ∬ D   x 2   d m = ∬ D   x 2   δ ( x , y ) d A

Então, basicamente: quando um problema pedir para você calcular o momento de inércia de uma região plana em relação a um eixo ( x ou y ), você vai aplicar uma dessas duas fórmulas e cair em uma integral dupla, que você vai resolver usando todos os conceitos de integral dupla que já viu até aqui.

É como uma integral qualquer! Memorize essas fórmulas, então, porque esse é o passo 1 desse tipo de questão, ok? Você vai aplicar a fórmula, montar a integral e resolvê-la.

As vezes ele pede o momento de inércia com relação a origem. Não se desespere! Basta somar os dois momentos de inércia que calculamos, ou seja

I o = I x + I y

Exemplo: Dada uma fina placa limitada pela reta x + y = 1 e pelos eixos x e y , sabendo que a sua densidade δ x , y = x 2 + 1 . Determine os momentos de inércia.

Passo 1: Primeiro vamos dar uma analisada na placa em questão:

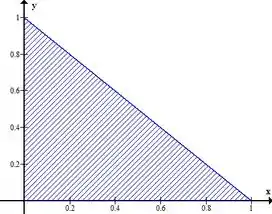
Não importa o tipo de região que faremos, vamos escolher o tipo I então, com isso:

0 ≤ y ≤ 1 - x

0 ≤ x ≤ 1

Passo 2: Para calcular os raios de rotação vamos precisar dos momentos de inércia, né? As fórmulas são essas aqui:

I x = ∬ D y 2 δ x , y d A

I y = ∬ D x 2 δ x , y d A

Logo:

I x = ∫ 0 1 ∫ 0 1 - x y 2 ( x 2 + 1 ) d y d x = ∫ 0 1 ∫ 0 1 - x x 2 y 2 + y 2 d y d x = 4 45

O mesmo para I y :

I y = ∫ 0 1 ∫ 0 1 - x x 2 x 2 + 1 d y d x = ∫ 0 1 ∫ 0 1 - x x 4 + x 2 d y d x = 7 60

Falta achar o momento de inercia em relação à origem, como fazemos isso? É bem tranquilo, é só fazer

I 0 = I x + I y

Logo:

I 0 = 4 45 + 7 60 = 37 180

Raio de Rotação

Todos os físicos, de modo geral, gostam muito de trabalhar com as questões concentrando todas informações do problema em um único ponto. Isso ajuda muito nos cálculos! O raio de rotação tem a ver com isso!

Ele nos diz a que distância de um eixo a massa total da placa pode estar concentrada em um ponto de forma a não mudar o momento de inércia. Muito abstrato, né? Por exemplo, R x é a distância ao eixo x que um ponto com toda a massa concentrada do objeto resulta em I x .

Se não entendeu isso não se preocupa muito! Esse é o significado físico, vamos trabalhar muito mais com as contas aqui em cálculo, na prática é só aplicar essas fórmulas aqui!

As fórmulas que vamos usar para calcular o Raio de rotação em relação aos eixos são essas aqui:

Em relação ao eixo x :

R x = I x M

Em relação ao eixo y :

R y = I y M

Podemos também achar o raio de rotação em relação a origem, para isso é só fazer:

R 0 = I 0 M

Exemplo

Vamos calcular o raio de rotação daquela região lá do início!

Passo 1: Para calcular os raios de rotação vamos precisar dos momentos de inércia, né? Como vimos lá em cima

I x = 4 45 ,     I y = 7 60 ,     I 0 = 3 7 180

Passo 3: A outra variável que precisamos calcular é a massa total da placa, dada pela fórmula

M = ∬ D δ x , y d A

Logo:

M = ∫ 0 1 ∫ 0 1 - x x 2 + 1 d y d x = 7 12

Passo 4: Agora é só substituir tudo nas fórmulas dos raios de rotação!

R x = I x M = 4 45 7 12 = 16 105 ≅ 0,39

R y = I y M = 7 60 7 12 = 12 60 ≅ 0,45

R 0 = I 0 M = 37 180 7 12 = 37 105 ≅ 0,59

Provavelmente na prova você não vai ter uma calculadora para calcular essa aproximação, só deixar como raiz mesmo. ;)

Viu que a parte demorada é calcular os momentos de inércia e a massa, né? Depois é só aplicar as fórmulas dos raios de rotação.

Agora vamos pros exercícios praticar isso um pouquinho!

Sacou a lógica? Então, vamos fazer uns exercícios!

Raio de Rotação

Exemplo

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Encontre o momento de inércia em relação ao eixo x de uma placa fina limitada pelas curvas x = y 2 e x = 2 y - y 2 se a densidade no ponto ( x , y ) for δ x , y = y + 1 .

Passo 1

A gente viu na teoria que o momento de inércia em relação ao eixo x pode ser encontrado pela fórmula:

I x = ∬ D   y 2   δ ( x , y ) d A

Então só temos que ver como que vai ficar a região para podermos resolver a integral.

Passo 2

A nossa região vai ser o interior da interseção de duas parábolas, que podemos esboçar assim:

Que podemos escrever tanto como tipo 1 , quanto tipo 2 , mas vamos escolher o tipo 2 porque tem equações mais simpáticas pros limites do x .

Dessa forma, vamos ter y variando entre 0 e aquele ponto de interseção entre as parábolas, dado em:

y 2 = 2 y - y 2 → 2 y 2 = 2 y

y 1 = 0           y 2 = 1

Então nossa região vai ser descrita por:

D = ( x , y ) ∈ R 2 | 0 ≤ y ≤ 1 , y 2 ≤ x ≤ 2 y - y 2

Agora é só calcular a integral!

Passo 3

Tinhamos a fórmula:

I x = ∬ D   y 2   δ x , y d A

⇒ ∫ 0 1 ∫ y 2 2 y - y 2 y 2 y + 1 d x d y

⇒ ∫ 0 1 ( y 3 + y 2 ) ∙ x │ y 2 2 y - y 2 d y = ∫ 0 2 ( y 3 + y 2 ) ∙ 2 y - y 2 - y 2 d y

= ∫ 0 1 ( y 3 + y 2 ) ∙ 2 y - 2 y 2 d y = ∫ 0 1 2 y 4 - 2 y 5 + 2 y 3 - 2 y 4   d y = ∫ 0 1 - 2 y 5 + 2 y 3   d y

⇒ - y 6 3 │ 0 1 + y 4 2 │ 0 1 = - 1 3 + 1 2 = - 1 ∙ 2 + 1 ∙ 3 6

⇒ 1 6

Resposta

I x = 1 6

Exercício Resolvido #2

Elaboração Própria

Encontre o momento de inércia em relação ao eixo x de um disco fino limitado pela circunferência x 2 + y 2 = a 2 se a densidade do disco em um ponto ( x , y ) for δ x , y = k x 2 + y 2 .

Passo 1

Vamos usar a fórmula que a gente viu na teoria:

I x = ∬ D   y 2   δ ( x , y ) d A

Mas a região é uma circunferência e a função da densidade também favorece coordenadas polares, então vamos ver como que fica isso!

Passo 2

Vamos lembrar que para usarmos coordenadas polares, fazemos a mudança de váriaveis:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

E a circunferência de raio a pode ser descrita como:

D = ( r , θ ) ∈ R 2 | 0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ a

Então, na verdade, o que vamos mesmo fazer é:

I x = ∬ D   y 2   δ x , y d A = ∫ 0 2 π ∫ 0 a r sin ⁡ θ 2   k ( r 2 )   r   d r d θ

⇒ k ∫ 0 2 π ∫ 0 a r 5 sin 2 ⁡ θ d r d θ

= k ∫ 0 2 π 1 - cos ⁡ 2 θ 2 d θ ∙ r 6 6 │ 0 a = k a 6 6 ∙ θ 2 │ 0 2 π - sin ⁡ 2 θ 4 │ 0 2

⇒ k a 6 6 ∙ π = π k a 6 6

Resposta

I x = π k a 6 6

Exercício Resolvido #3

UFF - Cálculo IIIA - Lista 1 - 15b

Seja uma lâmina delgada representada pela região D , determinada por y ≤ x , y ≥ - x , x 2 + y 2 ≥ 2 x e x 2 + y 2 ≤ 4 x . Se a densidade em cada ponto é dada por ρ x , y = 1 x 2 + y 2 , determine o momento de inércia em relação à origem.

Passo 1

Antes de qualquer coisa vamos determinar a figura que mostra D

A área vai ser entre as circunferências limitados pelas retas azuis.

Passo 2

Como tanto a função que vamos integrar como a região de integração possuem termos x 2 e y 2 , vamos utilizar coordenadas polares. Faremos, então:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Passo 3

Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.

Repara que o ângulo θ vai variar de um extremo da circunferência até o outro. Olha o desenho com o ângulo marcado

Então

θ 0 = - π 4

θ f = π 4

Vamos ver agora o valor de r . Pelas equações das circunferências temos

2 x ≤ x 2 + y 2 ≤ 4 x

Vamos trocar pelas coordenadas polares

2 r cos ⁡ θ ≤ r cos ⁡ θ 2 + r sen ⁡ θ 2 ≤ 4 r cos ⁡ θ

2 r cos ⁡ θ ≤ r 2 cos ⁡ θ 2 + sen ⁡ θ 2 ≤ 4 r cos ⁡ θ

2 r cos ⁡ θ ≤ r 2 ≤ 4 r cos ⁡ θ

Como r > 0

2 cos ⁡ θ ≤ r ≤ 4 cos ⁡ θ

Vamos ter

D = { ( r , θ ) | 2 cos ⁡ θ ≤ r ≤ 4 cos ⁡ θ ; -   π / 4 ≤ θ ≤ π / 4 }

Passo 4

O momento de inércia vai ser

I = ∬ D x 2 + y 2 ρ x , y d x d y = ∬ D x 2 + y 2 x 2 + y 2 d x d y = ∬ D x 2 + y 2 d x d y

Em coordenadas polares vamos ter

M = ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r cos ⁡ θ 2 + r sen ⁡ θ 2 d r d θ

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r 2 cos ⁡ θ 2 + sen ⁡ θ 2 d r d θ =

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r 2 d r d θ =

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r 2 d r d θ = ∫ - π / 4 π / 4 r 3 3 r = 2 sen ⁡ θ r = 4 cos ⁡ θ d θ = ∫ - π / 4 π / 4 4 cos ⁡ θ 3 3 - 2 cos ⁡ θ 3 3 d θ =

∫ - π / 4 π / 4 64 cos 3 ⁡ θ 3 - 8 cos 3 ⁡ θ 3 d θ = ∫ - π / 4 π / 4 56 cos 3 ⁡ θ 3 d θ = 56 3 ∫ - π / 4 π / 4 cos 3 ⁡ θ d θ

Vamos fazer essa integral separada,

Passo 5

∫ cos 3 ⁡ θ d θ = ∫ cos 2 ⁡ θ cos ⁡ θ d θ = ∫ 1 - sen 2 ⁡ θ cos ⁡ θ d θ

Agora fazemos

sen ⁡ θ = u

d u = cos ⁡ θ d θ

A integral vai ficar

∫ 1 - sen 2 ⁡ θ cos ⁡ θ d θ = ∫ 1 - u 2 d u

Resolvendo a integral temos

∫ 1 - u 2 d u = u - u 3 3

Voltando para θ

u - u 3 3 = sen ⁡ θ - s e n 3 θ 3

Passo 6

Voltando para a integral que tínhamos, vamos ter

56 3 ∫ - π / 4 π / 4 cos 3 ⁡ θ d θ = 56 3 sen ⁡ θ - s e n 3 θ   3 θ = - π / 4 θ = π / 4

= 56 3 sen ⁡ π 4 - sen 3 ⁡ π 4 3 - sen ⁡ - π 4 - sen 3 ⁡ - π 4 3

= 56 3 2 2 - 2 2 3 3 - - 2 2 - - 2 2 3 3

= 56 3 2 2 - 2 2 8 3 - - 2 2 - - 2 2 8 3

= 56 3 2 2 - 2 12 - - 2 2 + 2 12

= 56 3 5 2 12 - - 5 2 12

= 56 3 10 2 12

= 56 3 5 2 6

= 280 2 18

= 140 2 9

Resposta

140 2 9

Exercício Resolvido #4

Elaboração Própria

Uma placa retangular de densidade constante δ x , y = 1 ocupa a região limitadas pelas retas x = 4 e y = 2 no primeiro quadrante. O momento de inércia I a do retângulo em relação à reta y = a é dado pela integral:

I a = ∫ 0 4 ∫ 0 2 y - a 2 d y d x

Encontre o valor de a que minimiza I a .

Passo 1

Nesse exercício ele não usa o momento de inércia em relação a nenhum dos eixos, como estávamos vendo até agora, mas a uma reta paralela ao eixo x .

Mas como ele já dos dá a fórmula que vamos precisar a única coisa que temos que nos preocupar por enquanto é resolver essa integral:

I a = ∫ 0 4 ∫ 0 2 y - a 2 d y d x

Vamos ver como que fica!

Passo 2

Já temos tudo bonitinho, então é só sair resolvendo mesmo:

I a = ∫ 0 4 ∫ 0 2 y - a 2 d y d x = ∫ 0 4 d x ∙ ∫ 0 2 y - a 2 d y

⇒ 4 - 0 ∙ y - a 3 3 │ 0 2 = 4 ∙ 2 - a 3 3 - ( - a ) 3 3

= 4 3 ∙ 8 - 3 ∙ 4 ∙ a + 3 ∙ 2 ∙ a 2 - a 3 + a 3

= 4 3 8 - 12 a + 6 a 2

Essa é a expressão do momento de inércia I a em função do valor de a .

Passo 3

Mas como vamos saber o valor de a que vai nos dar o mínimo de I a ?

Pra responder isso vamos lembrar um conceito lá de Cálculo 1, de otimização.

Se derivarmos I a , vamos ter:

I a ' = 4 3 ( - 12 + 12 a )

E um ponto mínimo deve ser dar quando I a ' = 0 , então:

4 3 - 12 + 12 a = 0

⇒ 12 a = 12 → a = 1

Passo 4

Só para conferir, podemos fazer a segunda derivada de I a :

I a ' ' = 4 3 ∙ 12 = 16

Que é positivo, então podemos confirmar que se trata de um ponto mínimo local.

Resposta

a = 1

Exercício Resolvido #5

George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009

Encontre os raios de rotação em relação aos eixos coordenados e o raio de rotação polar de uma placa fina triangular limitada pelas retas y = x , y = - x e y = 1 se δ x , y = y + 1

Passo 1

Sabemos que a fórmula dos raios de rotação são as seguintes:

R x = I x M

R y = I y M

R 0 = I 0 M

Portanto vamos precisar calcular três integrais duplas! Dois momentos de inércia e uma para a massa total! I 0 podemos obter a partir da soma de I x e I y .

Vamos então descrever os limites da nossa região D , calcular os momentos de inércia e a massa e depois só jogar na fórmula do raio. Vamos lá?

Passo 2

O gráfico da nossa região triangular é esse aqui:

Escolhendo os limites de integração pelo tipo II:

- y ≤ x ≤ y

0 ≤ y ≤ 1

Passo 3

Para calcular o momento de inércia em relação ao eixo x usamos a integral:

I x = ∬ D y 2 δ x , y d A = ∫ 0 1 ∫ - y y y 2 y + 1 d x d y

= ∫ 0 1 ∫ - y y y 3 + y 2 d x d y

∫ 0 1 [ x y 3 + y 2 ] x = - y x = y d y

= ∫ 0 1 y - - y y 3 + y 2 d y = ∫ 0 1 2 y 4 + 2 y 3 d y

= 2 y 5 5 + 2 y 4 4 y = 0 y = 1 = 2 5 + 2 4 = 9 10

I x = 9 10

Passo 4

Para calcular o momento de inércia em relação ao eixo y usamos a integral:

I y = ∬ D x 2 δ x , y d A = ∫ 0 1 ∫ - y y x 2 y + 1 d x d y

= ∫ 0 1 x 3 3 x = - y x = y y + 1 d y

= ∫ 0 1 y 3 - - y 3 3 y + 1 d y = ∫ 0 1 2 y 3 3 y + 1 d y  

= 2 3 ∫ 0 1 y 4 + y 3 d y

= 2 3 y 5 5 + y 4 4 y = 0 y = 1 = 2 3 1 5 + 1 4 = 2 3 9 20 = 3 10

I y = 3 10

Sabendo que I x e I y podemos calcular I 0 :

I 0 = I x + I y = 3 10 + 9 10 = 12 10 = 6 5

I 0 = 6 5

Passo 5

Para calcular a massa M vamos usar a integral:

M = ∬ D δ x , y d A = ∫ 0 1 ∫ - y y ( y + 1 ) d x d y

= ∫ 0 1 y - - y y + 1 d y = ∫ 0 1 2 y ( y + 1 ) d y

= 2 ∫ 0 1 y 2 + y   d y

= 2 y 3 3 + y 2 2 y = 0 y = 1 = 2 1 3 + 1 2 = 2 5 6 = 5 3

M = 5 3

Passo 6

Agora é só jogar tudo nas fórmulas dos raios de rotação!

R x = I x M = 9 10 5 3 = 27 50 = 3 6 10

R y = I 0 M = 3 10 5 3 = 9 50 = 3 2 10

R 0 = I 0 M = 6 5 5 3 = 18 25 = 3 2 5

Resposta

R x = 3 6 10

R y = 3 2 10

R 0 = 3 2 5

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K