Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 38
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Passo 1
Para resolvermos questões relacionadas a centro de massa e momento de inercia precisamos da seguinte teoria :
Consideramos um sistema cuja massa total esta distribuída numa região do plano e não apenas num conjunto formado por um número finito de pontos, os conceitos de massa, centro de massa e momento são definidos por meio de integrais duplas. Por exemplo, consideremos uma lâmina fina tendo a forma de uma região D do plano e assumamos que a massa está distruibuida sobre essa lâmina com densidade (massa por unidade de área ) conhecida, isto é, existe uma função positiva definida em D tal que representa a massa por unidade de área em
Para o calculo do momento de inercia da lâmina, segue que
Se L é uma reta no plano da lâmina D, seja a distancia do ponto (x,y) em D à reta L. Defini-se momento de inercia por
Onde é a densidade em cada ponto
Passo 2
A figura que representa nossa situação é a seguinte:
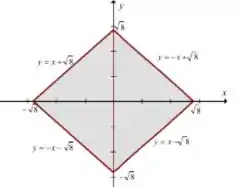
Desse modo podemos calcular o momento de inercia em relação ao eixo dos x