Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Momento de Inércia e Raio de Rotação de Sólidos

Ver Todos os Exercícios

Teoria

Como já vimos para regiões planas, o momento de inércia (ou segundo momento) de uma partícula em relação a um eixo é definido como m r 2 , onde m é a massa da partícula e r é a distância entre esse eixo e a partícula.

Trazendo esse conceito para três dimensões, podemos definir o momento de inércia de uma região sólida V com densidade de massa δ ( x , y , z ) . Para calcular o momento em relação ao eixo x , a distância dos pontos a esse eixo será dada por y 2 + z 2 . Portanto, temos:

I x = ∭ V   y 2 + z 2 2 d m = ∭ V   y 2 + z 2 δ ( x , y , z ) d V

Para o momento de inércia em relação a y , a distância passa a ser x 2 + z 2

I y = ∭ V   x 2 + z 2 δ ( x , y , z ) d V

Para o momento em relação a z , então:

I z = ∭ V   x 2 + y 2 δ ( x , y , z ) d V

Para ficar mais fácil de lembrar quais coordenadas que somamos ao quadrado em cada momento, repare que a coordenada do eixo é sempre a que não aparece. Exemplo: momento de inércia em relação ao eixo x , somamos y 2 + z 2 .

Então, basicamente: quando um problema pedir para você calcular o momento de inércia de uma região sólida em relação a um eixo ( x , y ou z ), você vai aplicar essas fórmulas e cair em alguma integral tripla. Daí você vai resolver usando todos os conceitos de integral tripla que você já viu até aqui (mudança esférica, cilíndrica etc).

É como uma integral qualquer! Memorize essas fórmulas, porque esse é o passo 1 desse tipo de questão, ok? Você vai aplicar a fórmula, montar a integral e resolvê-la. Vamos ver aqui um exemplo

Exemplo: Encontre o momento de inércia em relação ao eixo z do cubo com comprimento do lado 2 , um vértice localizado na origem, três arestas nos eixos coordenados e densidade constante k .

Passo 1: Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I z = ∭ W   x 2 + y 2 ρ ( x , y , z ) d V

Onde ρ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante k , logo:

I z = k ∭ W   x 2 + y 2 d V

Passo 2: Ótimo, agora vamos escrever matematicamente essa região.

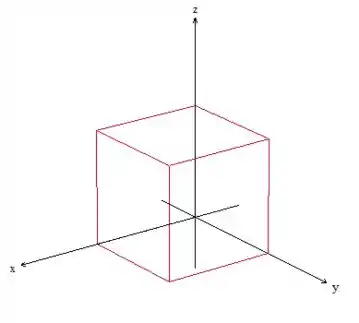
Bom, como se trata de um cubo, não temos muito trabalho para descrever essa região, todos os limites de integração são números:

I z = k ∫ 0 2 ∫ 0 2 ∫ 0 2 x 2 + y 2 d z d x d y

Passo 3: Agora vamos resolver isso aí.

I z = k ∫ 0 2 ∫ 0 2 z x 2 + y 2 0 2 d x d y

I z = 2 k ∫ 0 2 ∫ 0 2 x 2 + y 2 d x d y

I z = 2 k ∫ 0 2 x 3 3 + x y 2 0 2 d y

I z = 2 k ∫ 0 2 8 3 + 2 y 2 d y

I z = 2 k 8 y 3 + 2 y 3 3 0 2

I z = 2 k 16 3 + 16 3

I z = 64 k 3

Raio de Rotação

Acabamos de aprender como calcular o momento de inércia de um sólido, né? Existe uma propriedade física de sólidos associada ao segundo momento e que vamos ter que calcular em alguns problemas também: o raio de rotação!

O raio de rotação, por sua vez, é a distância em relação a um eixo em que podemos concentrar toda a massa de corpo de forma a termos o mesmo momento linear nesse eixo. Por exemplo, R x é a distância ao eixo x que um ponto com toda a massa concentrada do objeto resulta no mesmo I x .

Essa explicação é muito abstrata mesmo, se não entendeu tudo bem! Você praticamente só vai ter que aplicar uma fórmula nesse tipo de questão.

As fórmulas que vamos usar para calcular o Raio de rotação em relação aos eixos são essas aqui:

Em relação ao eixo x :

R x = I x M

Em relação ao eixo y :

R y = I y M

Em relação ao eixo z :

R z = I z M

Podemos também achar o raio de rotação em relação a origem, para isso é só fazer:

R 0 = I 0 M

O conceito novo desse capítulo é basicamente as fórmulas, o resto você já sabe.

Vamos fazer uns exercícios então!

Raio de Rotação

Exercícios Resolvidos

Exercício Resolvido #1

UNICAMP - Cálculo 2 - P2 2014 Manhã – 3

Encontre o momento de inércia em relação ao eixo z do cubo com comprimento do lado 2 , um vértice localizado na origem, três arestas nos eixos coordenados e densidade constante k .

Passo 1

Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I z = ∭ W   x 2 + y 2 ρ ( x , y , z ) d V

Onde ρ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante k , logo:

I z = k ∭ W   x 2 + y 2 d V

Passo 2

Ótimo, agora vamos escrever matemarticamente essa região.

Bom, como se trata de um cubo, não temos muito trabalho para descrever essa região, todos os limites de integração são números:

I z = k ∫ 0 2 ∫ 0 2 ∫ 0 2 x 2 + y 2 d z d x d y

Passo 3

Agora vamos resolver isso aí.

I z = k ∫ 0 2 ∫ 0 2 z x 2 + y 2 0 2 d x d y

I z = 2 k ∫ 0 2 ∫ 0 2 x 2 + y 2 d x d y

I z = 2 k ∫ 0 2 x 3 3 + x y 2 0 2 d y

I z = 2 k ∫ 0 2 8 3 + 2 y 2 d y

I z = 2 k 8 y 3 + 2 y 3 3 0 2

I z = 2 k 16 3 + 16 3

I z = 64 k 3

Resposta

64 k 3

Exercício Resolvido #2

Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1086 – 43

A tendência de um sólido para resistir a uma mudança no movimento rotatório em torno de um eixo é medida por seu momento de inércia em torno daquele eixo. Se um sólido ocupa uma região G num sistema de coordenadas x y z e se sua função densidade δ ( x , y , z ) for contínua em G , então os momentos de inércia em torno dos eixos x ,   y e z são denotados, respectivamente, por I x ,   I y e I z e são definidos por

I x = ∭ G y 2 + z 2 δ x ,   y ,   z d V

I y = ∭ G x 2 + z 2 δ x ,   y ,   z d V

I z = ∭ G x 2 + y 2 δ x ,   y ,   z d V

Determine o momento de inércia, I z , para o cilindro sólido x 2 + y 2 ≤ a 2 ,     0 ≤ z ≤ h de densidade δ constante.

Passo 1

Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I z = ∭ W   x 2 + y 2 δ ( x , y , z ) d V

Onde δ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante δ , logo:

I z = δ ∭ W   x 2 + y 2 d V

Passo 2

Agora vamos descrever o sólido matematicamente, como é um cilindro vamos usar coordenadas cilíndricas,

x = r ⋅ cos ⁡ θ y = r ⋅ s e n   θ z = z

Os limites de integração são,

0 ≤ z ≤ h

0 ≤ r ≤ a

0 ≤ θ ≤ 2 π

Passo 3

Por fim, vamos resolver a integral, substituindo para coordenadas cilíndricas d V = r d z d r d θ , logo:

I z = δ ∭ W   r 2 cos 2 ⁡ θ + r 2 s e n 2 θ r d z d r d θ

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1

I z = δ ∭ W   r 2 r d z d r d θ

I z = δ ∫ 0 2 π ∫ 0 a ∫ 0 h r 2   r d z d r d θ =   δ ∫ 0 2 π ∫ 0 a r 3   h d z d r d θ

I z =   δ ⋅ 2 π ⋅ h ⋅ r 4 4 0 a = δ π h a 4 2

Resposta

I z = δ π h a 4 2

Exercício Resolvido #3

Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1086 – 44

A tendência de um sólido para resistir a uma mudança no movimento rotatório em torno de um eixo é medida por seu momento de inércia em torno daquele eixo. Se um sólido ocupa uma região G num sistema de coordenadas x y z e se sua função densidade δ ( x , y , z ) for contínua em G , então os momentos de inércia em torno dos eixos x ,   y e z são denotados, respectivamente, por I x ,   I y e I z e são definidos por

I x = ∭ G y 2 + z 2 δ x ,   y ,   z d V

I y = ∭ G x 2 + z 2 δ x ,   y ,   z d V

I z = ∭ G x 2 + y 2 δ x ,   y ,   z d V

Determine o momento de inércia, I y , para o cilindro sólido x 2 + y 2 ≤ a 2 ,     0 ≤ z ≤ h de densidade δ constante.

(OBS: A diferença desse exercício pro anterior é que esse aqui pede o momento de inércia em y , o anterior pedia em z )

Passo 1

Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I y = ∭ W   x 2 + z 2 δ ( x , y , z ) d V

Onde δ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante δ , logo:

I y = δ ∭ W   x 2 + z 2 d V

Passo 2

Agora vamos descrever o sólido matematicamente, como é um cilindro vamos usar coordenadas cilíndricas,

x = r ⋅ cos ⁡ θ y = r ⋅ s e n   θ z = z

Os limites de integração são,

0 ≤ z ≤ h

0 ≤ r ≤ a

0 ≤ θ ≤ 2 π

Passo 3

Por fim, vamos resolver a integral, substituindo para coordenadas cilíndricas d V = r d z d r d θ , logo:

I y = δ ∭ W   r 2 cos 2 ⁡ θ + z 2 d V

I y = δ ∫ 0 2 π ∫ 0 a ∫ 0 h r 2 cos 2 ⁡ θ + z 2 r d z d r d θ =   δ ∫ 0 2 π ∫ 0 a r 3 cos 2 ⁡ θ ⋅ z + z 3 3 r 0 h   d r d θ

I y =     δ ∫ 0 2 π ∫ 0 a r 3 cos 2 ⁡ θ ⋅ h + h 3 3 r   d r d θ

I y =     δ ∫ 0 2 π r 4 4 cos 2 ⁡ θ ⋅ h + h 3 3 r 2 2 0 a   d θ

I y =     δ ∫ 0 2 π h a 4 4 cos 2 ⁡ θ + h 3 a 2 6   d θ    

Para não ficar muita informação, vamos calcular separadamente

∫ 0 2 π cos 2 ⁡ θ d θ

Usando o arco duplo, cos ⁡ 2 θ = 2 cos 2 ⁡ θ - 1 ,

∫ 0 2 π cos 2 ⁡ θ d θ = ∫ 0 2 π cos ⁡ 2 θ + 1 2 d θ = 1 2 s e n   2 θ + θ 0 2 π = π

Voltando para o momento de inércia,

I y =     δ h a 4 4 ∫ 0 2 π cos 2 ⁡ θ d θ + h 3 a 2 6 ∫ 0 2 π d θ  

Substituido o que calculamos,

I y = δ h a 4 4 π + h 3 a 2 3 π    

Resposta

I y = δ h a 4 4 π + h 3 a 2 3 π    

Exercício Resolvido #4

Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1086 – 45

A tendência de um sólido para resistir a uma mudança no movimento rotatório em torno de um eixo é medida por seu momento de inércia em torno daquele eixo. Se um sólido ocupa uma região G num sistema de coordenadas x y z e se sua função densidade δ ( x , y , z ) for contínua em G , então os momentos de inércia em torno dos eixos x ,   y e z são denotados, respectivamente, por I x ,   I y e I z e são definidos por

I x = ∭ G y 2 + z 2 δ x ,   y ,   z d V

I y = ∭ G x 2 + z 2 δ x ,   y ,   z d V

I z = ∭ G x 2 + y 2 δ x ,   y ,   z d V

Determine o momento de inércia, I z , para o cilindro sólido a 1 2 ≤ x 2 + y 2 ≤ a 2 2 ,     0 ≤ z ≤ h de densidade δ constante.

Passo 1

Como sabemos, o momento de inércia de um sólido W em relação ao eixo z é dado por:

I z = ∭ W   x 2 + y 2 δ ( x , y , z ) d V

Onde δ ( x , y , z ) é a função densidade. Porém, como o problema diz, a densidade é dada por uma constante δ , logo:

I z = δ ∭ W   x 2 + y 2 d V

Passo 2

Agora vamos descrever o sólido matematicamente, como é um cilindro vamos usar coordenadas cilíndricas,

x = r ⋅ cos ⁡ θ y = r ⋅ s e n   θ z = z

Os limites de integração são,

0 ≤ z ≤ h

a 1 ≤ r ≤ a 2

0 ≤ θ ≤ 2 π

Passo 3

Por fim, vamos resolver a integral, substituindo para coordenadas cilíndricas d V = r d z d r d θ , logo:

I z = δ ∭ W   r 2 cos 2 ⁡ θ + r 2 s e n 2 θ r d z d r d θ

Usando a relação fundamental da trigonometria, s e n 2 θ + cos 2 ⁡ θ = 1

I z = δ ∭ W   r 2 r d z d r d θ

I z = δ ∫ 0 2 π ∫ a 1 a 2 ∫ 0 h r 2   r d z d r d θ =   δ ∫ 0 2 π ∫ a 1 a 2 r 3   h d z d r d θ

I z =   δ ⋅ 2 π ⋅ h ⋅ r 4 4 a 1 a 2 = δ π h ( a 2 4 - a 1 2 ) 2

Resposta

I z = δ π h ( a 2 4 - a 1 2 ) 2

Exercício Resolvido #5

George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009 – modificado

Um sólido é limitado abaixo pelo cone z = x 2 + y 2 e acima pelo plano z = 1 . Encontre o raio de rotação desse sólido em relação ao eixo z se a densidade δ ( x , y , z ) = z

Passo 1

Raio de rotação em relação ao eixo z , esse a gente já sabe a fórmula, né?

R z = I z M

Beleza, então precisaremos calcular o momento de inércia I z :

I z = ∭ W x 2 + y 2 δ x , y , z d V

E depois calcular a massa M :

M = ∭ W δ x , y , z d V

Passo 2

Para fazer tudo isso vamos dar uma olhada no gráfico do nosso sólido:

Os limites de z são:

x 2 + y 2 ≤ z ≤ 1

Projetando o sólido no plano x y :

Olhando esses limites no plano xy e a integral do momento de inércia (Lembra que lá tem um x 2 + y 2 também?) dá pra ver que vale a pena fazer uma mudança de coordenada polar, então:

x = r cos ⁡ t

y = r sen ⁡ t

J = r

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Voltando para os limites de z , também, temos que:

x 2 + y 2 ≤ z ≤ 1

r ≤ z ≤ 1

Passo 3

Jogando esses limites na integral do momento de inércia em relação a z ficamos com:

I z = ∭ W x 2 + y 2 δ x , y , z d V = ∫ 0 2 π ∫ 0 1 ∫ r 1 r 2 z d z r d r d θ

= ∫ 0 2 π ∫ 0 1 r 3 z 2 2 z = r z = 1 d r d θ = ∫ 0 2 π ∫ 0 1 r 3 1 - r 2 2 d r d θ = 1 2 ∫ 0 2 π ∫ 0 1 r 3 - r 5 d r d θ

= 1 2 ∫ 0 2 π r 4 4 - r 6 6 r = 0 r = 1 d θ = 1 2 ∫ 0 2 π 1 4 - 1 6 d θ = 1 2 ∫ 0 2 π 2 24 d θ

= 1 24 . 2 π = π 12

I z = π 12

Passo 4

Calculando a massa do sólido:

M = ∭ W δ x , y , z d V = ∫ 0 2 π ∫ 0 1 ∫ r 1 z d z r d r d θ

= ∫ 0 2 π ∫ 0 1 z 2 2 z = r r = 1 r d r d θ = ∫ 0 2 π ∫ 0 1 1 - r 2 2 r d r d θ = 1 2 ∫ 0 2 π ∫ 0 1 r - r 3 d r d θ

= 1 2 ∫ 0 2 π r 2 2 - r 4 4 r = 0 r = 1 d θ = 1 2 ∫ 0 2 π 1 2 - 1 4 d θ = 1 2 ∫ 0 2 π 1 4 d θ

= 1 8 . 2 π = π 4

M = π 4

Passo 5

Voltando pra nossa fórmula de raio de rotação:

R z = I z M = π 12 π 4 = 1 3

Resposta

1 3

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .