Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 23

Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao plano X Y .

Passo 1

A gente tem que fazer em relação aos três eixos.

Pra isso a gente usa as integrais:

I x = ∭ D y 2 + z 2 δ x , y , z d V

I y = ∭ D x 2 + z 2 δ x , y , z d V

I z =   ∭ D x 2 + y 2 δ x , y , z d V

A densidade aqui pode ser escrita como δ x , y , z = K z .

O sólido é esse:

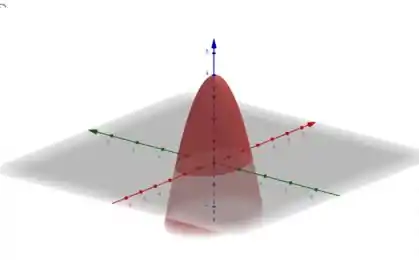
Considerando apenas a parte onde z > 0 .

Passo 2

Pra resolver as integrais, partimos da interseção do paraboloide com o plano z = 0 .

Vamos ter o círculo x 2 + y 2 = 4 .

Então, usamos coordenadas cilíndricas...

x = r c o s   θ y = r s e n   θ z = z

Onde aqui a gente tem:

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

0 ≤ z ≤ 4 - r 2

Montando a primeira integral então a gente tem:

I x = ∫ 0 2 π ∫ 0 2 ∫ 0 4 - r 2 r 2 s e n 2 θ + z 2 K z   r d z d r d θ

Passo 3

Vamos desenvolver então...

I x = K ∫ 0 2 π ∫ 0 2 ∫ 0 4 - r 2 r 3 z s e n 2 θ + z 3   r d z d r d θ

= K ∫ 0 2 π ∫ 0 2 [ r 3 z 2 2 s e n 2 θ + z 4 4 r ] 0 4 - r 2 d r d θ

= K ∫ 0 2 π ∫ 0 2 r 3 4 - r 2 2 2 s e n 2 θ + 4 - r 2 4 r 4   d r d θ

(na primeira a gente fez distributiva normal, na outra uma substituição u = 4 - r 2 )

= K ∫ 0 2 π 16 r 4 8 - 8 r 6 12 + r 8 16 0 2 s e n 2 θ + - 4 - r 2 5 40 0 2 d θ

= K ∫ 0 2 π 32 - 128 3 + 16 s e n 2 θ + 128 5   d θ

= K ∫ 0 2 π 16 3 s e n 2 θ + 128 5 d θ

= K 16 3 θ 2 - s e n   2 θ 4 0 2 π + 128 5 θ 0 2 π

= K 16 π 3 + 256 π 5

I x = 848 π 1 5 K

O momento de inércia em relação ao eixo x é esse.

Passo 4

Vamos para o de y   agora:

∫ 0 2 π ∫ 0 2 ∫ 0 4 - r 2 r 2 cos 2 ⁡ θ + z 2 K z   r d z d r d θ

Aqui só muda a componente θ , então as outras integrais a gente pode reutilizar (ô glória!!)...

Vamos pegar a partir daqui:

= K ∫ 0 2 π 16 3 cos 2 ⁡ θ + 128 5 d θ

= K 16 3 θ 2 + s e n   2 θ 4 + 128 5 θ 0 2 π

= K 16 3 π + 256 π 5

I y = 848 π 1 5 K

Prontinho! Momento de inércia em relação a y está ok.

Passo 5

Em relação ao eixo z agora pra acabar:

I z = ∫ 0 2 π ∫ 0 2 ∫ 0 4 - r 2 r 2 cos 2 ⁡ θ + r 2 s e n 2 θ K z   r d z d r d θ

(lembrando que s e n 2 θ + cos 2 ⁡ θ )

= K ∫ 0 2 π ∫ 0 2 ∫ 0 4 - r 2 r 3 z   d z d r d θ

= K ∫ 0 2 π ∫ 0 2 4 - r 2 2 2 r 3 d r d θ

(a gente já fez essa integral lá em cima)

= K ∫ 0 2 π 16 3 d θ

= K 16 3 2 π

I z = 32 π 3

Pronto! Esse é o momento de inércia em relação ao eixo z . Todos calculados então😉

Resposta

I x = 848 π 15 K

I y = 848 π 15 K

I z = 32 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inércia em relação ao eixo z .O hemisfério x 2 + y 2 + z 2 ≤ 1 , z ≥ 0 ; ρ x , y , z = x 2
Escreva, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inércia em relação ao eixo z .O sólido do Exercício 21; ρ x , y , z = x 2 + y 2
Seja E o sólido no primeiro octante limitado pelo cilindro x 2 + y 2 = 1 e pelos planos y = z , x = 0 e z = 0 com função densidade ρ x , y , z = 1 + x + y + z . Use um sistema de computação algébrica
Utilize coordenadas esféricas.Seja H um hemisfério sólido de raio a cuja densidade em qualquer ponto é proporcional à distância ao centro da base.a) Determine a massa de H .b) Determine o centro de ma
Utilize coordenadas esféricas.a) Determine o centroide do hemisfério sólido homogêneo de raio a .b) Determine o momento de inércia do sólido da parte (a) em relação a um diâmetro de sua base.