Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integração por Partes

Ver Todos os Exercícios

Teoria

A integração por partes é (mais uma) técnica de integração! 🥲

Mas calma, vem comigo que você vai aprender TUDO o que você precisa saber sobre integração por partes para arrasar na prova!

Quando usar a Integração por Partes?

A integração por partes é uma técnica de integração utilizada para integrar um produto de funções. Essa técnica é mais útil quando temos um produto de funções diferentes, como por exemplo, logaritmo multiplicado por função trigonométrica, exponencial multiplicada por polinômio, e assim por diante, sendo uma delas fácil de integrar e a outra mais fácil de derivar.

Mas, vamos ao que interessa, a Fórmula da integração por partes:

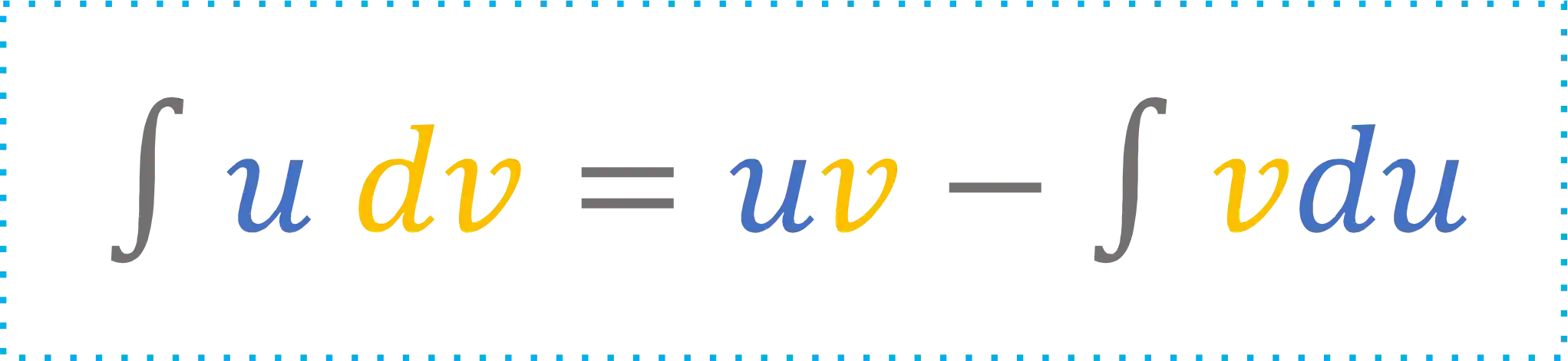
Integral por partes: fórmula
Integral por partes: fórmula

-WHAT?? 😵‍💫😵‍💫😵‍💫

Calma! Se liga nesse vídeozinho que o Responde Aí preparou especialmente pra você entender integração por partes de uma vez por todas! 👇👇👇

📢Clique para saber mais:

Como Utilizar a Integração por Partes?

Vamos pegar uma integral de exemplo e ir fazendo passo a passo de como devemos aplicar essa integração por partes!

Passo 1: Decidir quem Vai ser e quem vai ser

Precisamos olhar pra expressão da nossa integral e escolher dentre aquele produto de funções a que seja mais fácil de derivar e vamos chamar ela de , e aí a que for mais fácil de integrar vamos chamar de .

Mas como escolher quem vai ser o e quem vai ser o ? Vamos dar um macete aqui: Vamos escolher a função de vamos chamar de seguindo a ordem LIATE:

LIATE: Integração por partes
LIATE: Integração por partes

Então, você escolhe seguinte essa ordem de preferência, e a função que sobrar será o . Para o nosso exemplo, temos um polinômio e uma exponencial, então vamos escolher assim:

PASSO 2: Calcular , derivando a função

Para o nosso exemplo:

PASSO 3: Calcular integrando a função

Para o nosso exemplo:

PASSO 4: Aplicar a fórmula de integração por partes

Para o nosso exemplo:

PASSO 5: Calcular a integral

Para o nosso exemplo:

PASSO 6: Calcular o resultado da integral que desejamos

Para o nosso caso:

Ohh, não podemos esquecer de colocar a constante no final, porque é uma integral indefinida, beleza?

Mas no geral, é só seguir esse passo a passo que vai dar bom!

Vídeo: Exercício Resolvido

Agora pra fechar com chave de ouro, se liga nesse exercício de Integração por Partes resolvido em vídeo 👇👇👇

Bora praticar com mais exercícios? 😉

Como Utilizar a Integração por Partes?

Passo 1: Decidir quem Vai ser e quem vai ser

PASSO 2: Calcular , derivando a função

PASSO 3: Calcular integrando a função

PASSO 4: Aplicar a fórmula de integração por partes

PASSO 5: Calcular a integral

PASSO 6: Calcular o resultado da integral que desejamos

Vídeo: Exercício Resolvido

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Calcule a integral.

∫ x 2 cos ⁡ 3 x d x

Passo 1

Fazer por partes é a boa, função polinomial, algébrica ( x 2 ) e uma função trigonométrica ( cos ⁡ 3 x ).Vamos seguir os passos da integração por partes.

Passo 2

∫ x 2 cos ⁡ 3 x d x

1. Chamar uma parte da integral de u e outra de d v , LIATE!

u = x 2     ( a l g é b r i c a l ,   A ) d v = c o s   3 x   d x     ( t r i g o n o m é t r i c a ,   T )

2. Calcular d u derivando u . E calcular v integrando d v .

d u = 2 x   d x v = 1 3 sen ⁡ 3 x

3. Fazer ∫ u d v = u v - ∫ v d u

∫ x 2 cos ⁡ 3 x d x = 1 3 x 2 ⋅ sen ⁡ 3 x - ∫ 2 3 x ⋅ sen ⁡ 3 x d x =

= 1 3 x 2 ⁡ sen ⁡ 3 x - 2 3 ∫ x sen ⁡ 3 x d x

4. Verificar como calcular a integral ∫ v d u . É para calcular por partes de novo!! Se prepare para, às vezes, ter que usar a integração por partes duas ou mais vezes num mesmo problema.

Passo 3

5. Calcular!

Vamos chamar ∫ x sen ⁡ 3 x d x de I .

Calculando I por partes:

u = x → d u = d x d v = sen ⁡ 3 x → v = - 1 3 cos ⁡ 3 x

Então:

I = - 1 3 x ⋅ cos ⁡ 3 x - ∫ - 1 3 cos ⁡ 3 x d x = - 1 3 x ⋅ cos ⁡ 3 x + 1 3 ∫ cos ⁡ 3 x d x =

= - 1 3 x cos ⁡ 3 x + 1 9 sen ⁡ 3 x

Logo:

∫ x 2 cos ⁡ 3 x d x = 1 3 x 2 sen ⁡ 3 x - 2 3 - 1 3 x cos ⁡ 3 x + 1 9 sen ⁡ 3 x =

= 1 3 x 2 sen ⁡ 3 x + 2 9 x cos ⁡ 3 x - 2 27 sen ⁡ 3 x + C

Resposta

∫ x 2 cos ⁡ 3 x d x = 1 3 x 2 sen ⁡ 3 x + 2 9 x cos ⁡ 3 x - 2 27 sen ⁡ 3 x + C

Exercício Resolvido #2

PUC-RJ - Cálculo 1 - P4 2010.1 - 2 a

Calcule:

∫ x arctg ⁡ x 2 d x

Passo 1

Cara, não tem erro, x 2 ' = 2 x , correto? Então podemos fazer uma substituição que resolve bastante coisa:

t = x 2 → d t = 2 x   d x     ;     x   d x = d t 2

∫ x arctg ⁡ x 2 d x = ∫ arctg ⁡ t d t 2

= 1 2 ∫ arctg ⁡ t d t

Agora tudo se resume em fazer a integral desse arco-tangente. Bom, nesse cara aí temos uma inversa trigonométrica e um polinômio (considerando que está multiplicado por 1 , um polinômio de grau 0 ), a boa é seguir pela integral por partes.

Passo 2

Pelo LIATE escolhemos o nosso u sendo a Inversa trigonométrica e a algébrica, polinomial, será nosso d v :

u = arctg ⁡ t → d u = d t 1 + t 2

d v = d t → v = t

Agora é só usar a fórmula da integral por partes:

∫ arctg ⁡ t d t = t arctg ⁡ t - ∫ t   d t 1 + t 2

Passo 3

A integral que sobrou pode ser resolvida por substituição:

y = 1 + t 2

d y = 2 t   d t → t   d t = d y 2

Fica assim,

∫ t   d t 1 + t 2 = ∫ d y 2 y = ln ⁡ y 2

= ln ⁡ 1 + t 2 2

Passo 4

Então a integral toda fica assim:

1 2 ∫ arctg ⁡ t d t = 1 2 t arctg ⁡ t - ln ⁡ 1 + t 2 2 + C

Como t = x 2 :

∫ x arctg ⁡ x 2 d x = 1 2 x 2 arctg ⁡ x 2 - ln ⁡ 1 + x 4 2 + C

Resposta

∫ x arctg ⁡ x 2 d x = 1 2 x 2 arctg ⁡ x 2 - ln ⁡ 1 + x 4 2 + C

Exercício Resolvido #3

UERJ – Cálculo 1 - Lista Integrais Professora Renata - 3

Calcule a Integral:

∫ x 4 ln ⁡ x 2 d x

Passo 1

Como polinômio desse jeito e logarítmica não tem nenhuma relação direta, vou pensar em Integral por partes. Pelo LIATE eu devo chamar o log. de u e o resto vai ser d v :

u = ln ⁡ x 2           ;           d u = 2 ln ⁡ x x d x

d v = x 4 d x           ;           v = x 5 5

∫ x 4 ln ⁡ x 2 d x = ln ⁡ x 2 x 5 5 - ∫ x 5 5 2 ln ⁡ x x d x

1 5 x 5 ln ⁡ x 2 - 2 ∫ x 4 ln ⁡ x d x

Passo 2

Sobrou uma integral que novamente mistura log e polinômio. Mesmo processo, amigo:

u = ln ⁡ x         ;           d u = d x x

d v = x 4 d x           ;           v = x 5 5

∫ x 4 ln ⁡ x d x = ln ⁡ x x 5 5 - ∫ x 5 5 d x x = ln ⁡ x x 5 5 - 1 5 x 5 5

Passo 3

Vou trazer de volta para a equação inicial:

∫ x 4 ln ⁡ x 2 d x = 1 5 x 5 ln ⁡ x 2 - 2 ∫ x 4 ln ⁡ x d x

= 1 5 x 5 ln ⁡ x 2 - 2 ln ⁡ x x 5 5 + 2 x 5 25

= x 5 5 ln ⁡ x 2 - 2 ln ⁡ x 5 + 2 25

Colocando a constante no final da integral: ∫ x 4 ln ⁡ x 2 d x = x 5 5 ln ⁡ x 2 - 2 ln ⁡ x 5 + 2 25 + C

Resposta

∫ x 4 ln ⁡ x 2 d x = x 5 5 ln ⁡ x 2 - 2 ln ⁡ x 5 + 2 25 + C

Exercício Resolvido #4

USP - Cálculo 1 - P3 2012 - 1 b

Calcule:

  ∫ sec 2 ⁡ x ln ⁡ cos ⁡ x d x

Passo 1

Como eu não vejo nenhuma substituição de cara para resolver esse cara, eu vou pensar que esse é um produto entre uma trigonométrica e um logaritmo, funções que não dialogam diretamente. A resolução de integrais que mexe com integrais de funções diferentes misturadas é a resolução por partes. Vamos seguir o LIATE para escolha do u para aplicar nossa fórmula da integral por partes, L de logaritmo vem antes de T de trigonométrica, então o u será o log. O que sobrar será d v :

u = ln ⁡ cos ⁡ x → d u = cos ⁡ x ' cos ⁡ x

= - sen ⁡ x cos ⁡ x = - tg ⁡ x d x

d v = sec 2 ⁡ x d x → v = tg ⁡ x

∫ sec 2 ⁡ x ln ⁡ cos ⁡ x d x = ln ⁡ cos ⁡ x tg ⁡ x - ∫ tg ⁡ x - tg ⁡ x d x

Passo 2

Agora é só resolver a integral que sobrou do lado esquerdo:

ln ⁡ cos ⁡ x tg ⁡ x - ∫ tg ⁡ x - tg ⁡ x d x

= ln ⁡ cos ⁡ x tg ⁡ x + ∫ tg 2 ⁡ x d x

Sabemos que tg 2 ⁡ x não tem uma integral direta, porém sec 2 ⁡ x até tem. Se há uma relação trigonométrica que diz que 1 + tg 2 ⁡ x = sec 2 ⁡ x , podemos reescrever tudo assim:

= ln ⁡ cos ⁡ x tg ⁡ x + ∫ - 1 + sec 2 ⁡ x d x

= ln ⁡ cos ⁡ x tg ⁡ x - x + tg ⁡ x + C

Resposta

∫ sec 2 ⁡ x ln ⁡ cos ⁡ x d x = ln ⁡ cos ⁡ x tg ⁡ x - x + tg ⁡ x + C

Exercício Resolvido #5

USP - Cálculo 1 - P3 2014.1 – 1a

Calcule as seguintes integrais:

  ∫ ln ⁡ ( x 2 + 4 x + 5 ) d x

Passo 1

Bom, ln ⁡ ( x ) é um negócio meio complicado de integrar de primeira. A saída é reparar que o d x ali é como se fosse um polinômio de grau 0 . Então teríamos a função logarítmica multiplicada por 1 d x . Assim,

∫ ln ⁡ x 2 + 4 x + 5 ∙ 1 d x

Pronto! Encontramos dois tipos de funções diferentes. Sendo assim, cabe usar a Integral por Partes!

O dilema sobre quem vamos chamar de u e quem será o nosso d v , vai depende de quem for mais fácil de integrar. Afinal a gente aqui quer simplificar né? Então vamos usar o macete do LIATE.

Opa, o Logaritmo será a nossa primeira opção para escolher o u , correto? Então o restante será nosso d v .

u = ln ⁡ ( x 2 + 4 x + 5 )   ; d v = d x

d u = 2 x + 4 x 2 + 4 x + 5 d x     ; v = x

Agora vamos jogar na fórmula,

∫ ln ⁡ ( x 2 + 4 x + 5 ) d x = u . v - ∫ v . d u

∫ ln ⁡ ( x 2 + 4 x + 5 ) d x = ln ⁡ x 2 + 4 x + 5 x - ∫ x 2 x + 4 x 2 + 4 x + 5 d x

= ln ⁡ x 2 + 4 x + 5 x - 2 ∫ ( x 2 + 2 x ) x 2 + 4 x + 5 d x

A partir de agora só precisamos resolver essa integral e pronto.

Passo 2

∫ ( x 2 + 2 x ) x 2 + 4 x + 5 d x

Repara que temos uma fração com grau dois em cima e grau dois embaixo. Vamos dar uma mexida nessa função? Vamos escrever o nosso ( x 2 + 2 x ) como uma diferença de polinômios utilizando o nosso denominador. Repara que,

x 2 + 2 x = x 2 + 4 x + 5 + ( - 2 x - 5 )

Agora vamos substituir na nossa função,

( x 2 + 2 x ) x 2 + 4 x + 5 = x 2 + 4 x + 5 + ( - 2 x - 5 ) x 2 + 4 x + 5 = 1 + ( - 2 x - 5 ) x 2 + 4 x + 5

Ok, já melhorou. Em cima ficamos com grau 1 e embaixo com grau 2. Mas e para integrar esse negócio?

∫ 1 + ( - 2 x - 5 ) x 2 + 4 x + 5 = ∫ 1 d x + ∫ ( - 2 x - 5 ) x 2 + 4 x + 5 d x

Vamos resolver cada integral,

∫ 1 d x = x + C

Agora vamos para a mais complicada! Mas aí vem o pulo do gato, repara na substituição que eu vou fazer:

∫ ( - 2 x - 5 ) x 2 + 4 x + 5 d x = ∫ ( - 2 x - 5 ) ( x 2 + 4 x + 4 ) + 1 d x = ∫ ( - 2 x - 5 ) x + 2 2 + 1 d x

u = x + 2   ; d u = d x

∫ ( - 2 x - 5 ) x + 2 2 + 1 d x = ∫ ( - 2 ( u - 2 ) - 5 ) u 2 + 1 d u = ∫ ( - 2 u - 1 ) u 2 + 1 d u

= ∫ - 2 u u 2 + 1 d u - ∫ 1 u 2 + 1 d u

= - ln ⁡ u 2 + 1 - arctg ⁡ u = - ln ⁡ ( x 2 + 4 x + 5 ) - arctg ⁡ x + 2

Foi? Só repetindo tudo bonitinho aqui embaixo e não esquecendo que tínhamos um somatório, temos

∫ ( x 2 + 2 x ) x 2 + 4 x + 5 d x = ∫ 1 d x + ∫ ( - 2 x - 5 ) x 2 + 4 x + 5 d x = x - ln ⁡ x 2 + 4 x + 5 - arctg ⁡ x + 2 + C

Passo 3

Bom, vamos voltar para o pedaço de antes:

∫ ln ⁡ x 2 + 4 x + 5 d x = ln ⁡ x 2 + 4 x + 5 x - 2 ∫ x 2 + 2 x x 2 + 4 x + 5 d x

∫ ln ⁡ ( x 2 + 4 x + 5 ) d x = ln ⁡ x 2 + 4 x + 5 x - 2 ∫ 1 + - 2 x - 5 x 2 + 4 x + 5 d x

= ln ⁡ x 2 + 4 x + 5 ( x ) - 2 x - ln ⁡ x 2 + 4 x + 5 - arctg ⁡ x + 2

ln ⁡ x 2 + 4 x + 5 x + 2 - 2 x + 2 arctg ⁡ x + 2 + C

Resposta

∫ ln ⁡ ( x 2 + 4 x + 5 ) d x = ln ⁡ x 2 + 4 x + 5 x + 2 - 2 x + 2 arctg ⁡ x + 2 + C

Exercício Resolvido #6

Elaboração própria

Resolva a integral:

∫ e 2 x sen ⁡ x   d x

Passo 1

A tentativa do método da integração por partes é super recomendada aqui, pois trata-se de um produto de uma função exponencial ( e 2 x ) por uma função trigonométrica ( sen ⁡ x ).

Vamos seguir os passos da integração por partes.

Passo 2

∫ e 2 x sen ⁡ x   d x

1. Chamar uma parte da integral de u e outra de d v . LIATE!

u = sen ⁡ x     ( t r i g o n o m é t r i c a ,   T ) d v = e 2 x d x         ( e x p o n e n c i a l ,   E )

2. Calcular d u derivando u . E calcular v integrando d v .

d u = cos ⁡ x d x v = 1 2 e 2 x

3. Fazer ∫ u d v = u v - ∫ v d u

∫ e 2 x sen ⁡ x d x = 1 2 e 2 x sen ⁡ x - ∫ 1 2 e 2 x cos ⁡ x d x

4. Verificar como calcular a integral ∫ v d u . Vamos ter que usar o método da integração por partes de novo. Repare que temos um produto, de novo, de uma função exponencial por uma função trigonométrica

Passo 3

5. Calcular!

Seja I = ∫ 1 2 e 2 x cos ⁡ x d x .

Calculando pelo método da integração por partes:

u = cos ⁡ x → d u = - sen ⁡ x   d x d v = 1 2 e 2 x d x → v = 1 4 e 2 x

Então:

I = 1 4 e 2 x cos ⁡ x - ∫ - 1 4 e 2 x sen ⁡ x   d x =

= 1 4 e 2 x cos ⁡ x + 1 4 ∫ e 2 x sen ⁡ x   d x

Passo 4

Ora, olhe onde chegamos! Temos que calcular a integral do enunciado. Repare:

∫ e 2 x sen ⁡ x d x = 1 2 e 2 x sen ⁡ x - 1 4 e 2 x cos ⁡ x - 1 4 ∫ e 2 x sen ⁡ x   d x

Parece que chegamos em uma encruzilhada! Mas, não! Com um olhar mais atento, podemos perceber que podemos tratar   ∫ e 2 x sen ⁡ x   d x como uma variável a ser calculada. Assim, multiplico tudo por 4 :

4 ∫ e 2 x sen ⁡ x d x = 2 e 2 x sen ⁡ x - e 2 x cos ⁡ x - ∫ e 2 x sen ⁡ x d x

5 ∫ e 2 x sen ⁡ x d x = 2 e 2 x sen ⁡ x - e 2 x cos ⁡ x

∫ e 2 x sen ⁡ x d x = 2 5 e 2 x sen ⁡ x - 1 5 e 2 x cos ⁡ x + C

Resposta

∫ e 2 x sen ⁡ x d x = 2 5 e 2 x sen ⁡ x - 1 5 e 2 x cos ⁡ x + C

Exercício Resolvido #7

Elaboração própria

Resolva a integral:

∫ e sen ⁡ x cos ⁡ sen ⁡ x cos ⁡ x d x

Passo 1

A tentativa do método da integração por partes é super recomendada aqui, pois trata-se de um produto de uma função exponencial por uma função trigonométrica.

Vamos seguir os passos da integração por partes.

Mas repara que antes temos que fazer uma substituição, temos sen ⁡ x no exponencial e dentro de um dos cossenos. E cos ⁡ x do lado de fora, que é a sua derivada. Então vamos começar fazendo a substituição

y = sen ⁡ x

d y = cos ⁡ x d x