Introdução e Definição de Integral
Teoria
A Integral como Área
Esse é um capítulo bem importante para entendermos o conceito de Integrais.
A primeira coisa que devemos entender é que uma Integral representa o valor de uma área, beleza?!
Se pararmos para analisar, tem algumas áreas que conseguimos calcular de boa, como essas aqui embaixo:
Agora, imagina que queremos calcular a área azul abaixo:
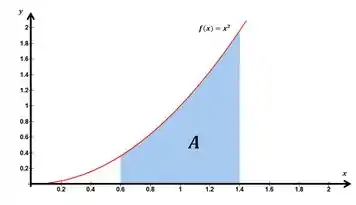
Talvez você não faça ideia de como calcular a área disso... rs.
No caso da figura acima, queremos calcular a área embaixo da função entre e .
Para calcular áreas nesse tipo de situação podemos utilizar a Soma de Riemann, porém isso será abordado mais pra frente! O importante agora é fixar a ideia que integrar é mais uma forma de calcular áreas.
Notação
Vamos entender essa notação de integral de forma mais geral:
é chamado de integrando que é a função que queremos a área;
é o limite inferior, que é onde começa o intervalo que queremos a área;
é o limite superior, que é onde termina o intervalo que queremos a área; mostra que estamos integrando na variável (se fosse , por exemplo, estaríamos integrando em ).
Show de bola?!
É importante a gente saber também que existem dois tipos de integrais: as integrais definidas e as indefinidas.
A Integral Definida resulta em um número, um valor. Essa integral acontece quando os limites de integração são números também, ou seja, na maioria dos casos.
A Integral Indefinida resulta em uma função. Nela, não há os limites de integração, o que resulta em uma outro função que chamamos de Primitiva da função .
Sinal da Integral
Essa é uma parte tranquila da matéria, mas pode se tornar problemática se não estiver bem clara. As integrais podem ter valores positivos e negativos! Sim, é verdade rs!
Como já conversamos anteriormente, a integral representa uma área delimitada por uma função, porém essa função pode estar na parte negativa do plano cartesiano, observe:
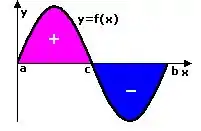
Quando a função está abaixo do eixo , o valor da integral é negativo! Quando a função está acima do eixo , o valor da integral é positivo!
e
Portanto, temos que ter cuidado se quisermos calcular áreas e não integrais, pois as áreas são sempre positivas (não existe área negativa).
Por exemplo:
Note que como (um número negativo) então na hora de calcularmos a área azul precisamos incluir o sinal negativo, para que o valor da área seja positivo.
Se quisermos calcular a área total, ou seja, temos que calcular :
Assim,
Beleza?!
Vamos praticar então?!
Notação
Sinal da Integral
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ - Cálculo 1 - P3 2010.1 – 4a - modificado
Considere o seguinte gráfico da função
Sabendo que as áreas das regiões , , , e são:
.
Calcule:
Passo 1
Bom, vamos lá! O problema quer que a gente calcule várias integrais, mas ainda não sabemos calcular isso. Agora, o que o problema deu pra gente foram as áreas das regiões do gráfico!
Então uma coisa que a gente precisa saber que que a integral de uma função representa a área abaixo da curva dessa função! Como ele deu as área pra gente, aí podemos calcular as integrais.
Na primeira integral temos
Isso vai ser a área de à . Sabemos que a área dessa região é , logo a integral vai ser:
Passo 2
A integral seguinte, temos:
Usando a mesma lógica, vamos ver que a integral vai ser a soma das áreas das regiões e .
Agora, precisamos observar uma coisa muito importante, aqui, temos uma parte da função acima do eixo e outra abaixo.
Apesar de não existir área negativa, existe integral negativa. Portanto, temos que levar em consideração que a área de vai fazer uma contribuição negativa por estar abaixo do eixo x. A integral então vai ser:
Passo 3
Por último temos:
Como a gente já calculou , podemos separar como:
Que dá no mesmo que somar todas as áreas, como você preferir... mas temos que lembrar que a área de também está abaixo do eixo x. Então ficamos com:
Substituindo temos:
Resposta
Exercício Resolvido #2
Elaboração própria
Analise as seguintes expressões:
Sabendo que elas são válidas e que , e são funções contínuas em , calcule os seguintes itens:
Passo 1
Partiu fazer? Partiu! Vai, analisa comigo: ele está dando um monte de integrais definidas com funções genéricas , e e pedindo o valor de integrais que envolvem essas integrais. Tá na cara que temos que usar propriedades de integrais definidas, você não acha, não?
Então vamos lá!
Passo 2
Na letra , vamos começar usando as propriedades de integrais definidas que aprendemos para quebrar aquela expressão que ele está pedindo, porque aí vai ficar muito mais fácil entender o que você vai usar.
Olha o que ele está pedindo:
Já sabemos que:
Portanto, podemos reescrever o que ele está pedindo como:
Passo 3
E agora? O que podemos fazer com isso?
Não temos nem . O que eu faço? Socorro! Calma, não se desespere! Ainda existem outras propriedades de integrais que podemos usar.
Vamos começar pela , que está mais fácil de visualizar.
Observe que temos
Concorda que se invertemos os limites de integração, teremos , que é o que nos interessa? E como fazemos isso? Lançamos mão daquela linda propriedade:
Logo:
Como:
Temos:
Passo 4
E quanto à ? Olha só as duas integrais que nós temos do enunciado:
A integral que nós queremos é . Nós temos 2 no limite superior de integração de uma integral e 3 no limite superior da outra. Além disso, o -1 aparece como limite de integração nas duas integrais. Dá para sentir aquele gostinho de que é para usar aquela propriedade de juntar os limites de integração?
Mas repara que, do jeito que as integrais estão, não dá para usar essa propriedade. Porque o número equivalente ao , que é o limite de integração que tem que ser igual nas duas integrais, é limite inferior nas duas e, para usar essa propriedade, ele tem que ser limite inferior da primeira e limite superior da segunda.
Olha aí a propriedade de inverter os limites de integração nos salvando de novo!
Agora, temos:
E queremos:
Podemos finalmente utilizar as propriedades de juntar os limites de integração:
Passo 5
Agora que já sabemos e , podemos finalmente juntar tudo:
Passo 6
Agora vamos à letra
Essa letra é meio estranha à primeira vista. O que acontece é que ele coloca uma função da variável no limite da integral. Mas isso dá menos dor de cabeça do que parece. Observe que a variável dentro da integral é . Aquela função de em nada atrapalha a integral.
Ele nos dá . Quando ele pede , simplesmente temos que substituir por e aí teremos o limite superior da integral. A partir daí, resolvemos normalmente.
Passo 7
Fazendo
Nesse caso, olha como fica a integral:
Opa, essa a gente já calculou, lembra? Depois de utilizar as propriedades de integrais na letra , chegamos à conclusão de que essa integral valia .
Pronto!
Resposta
a)
b)
Exercício Resolvido #3
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pp 419 - 9
Se , e , determine:
Passo 1
Ele está dando integrais definidas com funções genéricas e e pedindo o valor de integrais que envolvem essas integrais. Hum, acho que isso tá com cheiro de propriedades de integrais!
Passo 2
Letra a)
Veja bem:
Queremos e temos o valor da integral
A única coisa que muda é a constante multiplicando , certo? Os limites de integração são os mesmos. Então que tal usarmos essa propriedade aí embaixo?
Do enunciado, sabemos que:
Logo:
Pronto!
Passo 3
Letra b)
Queremos e temos o valor das integrais e
Essa questão é diferente da anterior. Agora, além da constante multiplicando , os limites de integração também mudam. Observe que queremos calcular uma integral com limite inferior 2 e temos o valor de duas integrais com o limite inferior igual a -2, sendo que uma delas tem limite superior igual a 2 e a outra limite superior igual a 5.
Isso nos leva a pensar na possibilidade de usar aquela propriedade de juntar intervalor de integração:
Pensa aqui comigo se eu não posso escrever:
Bem, o que temos não é a integral de e sim
Então para podermos usar a propriedade acima, primeiro devemos utilizar aquela propriedade de inverter os limites de integração:
Nesse caso:
No item , já calculamos
Do item :
Logo:
Do enunciado:
Então:
Passo 4
Letra c)
Agora devemos calcular
Temos o valor de
Aqui a constante multiplicando a função muda, bem como a ordem dos limites de integração. Portanto, utilizamos as propriedades abaixo:
Temos:
Do enunciado, sabemos que:
Logo:
E então:
Passo 5
Letra d)
Queremos e temos o valor de , calculado no item
Nesse caso, a única coisa que difere é a constante multiplicando a função . Mais uma vez, podemos utilizar a propriedade:
Passo 6
Letra e)
Queremos calcular e temos os valores de (calculado no item e o valor de (calculado no item .
A primeira coisa que devemos notar é que podemos reescrever essa soma da seguinte forma:
Utilizando a propriedade:
(Ufa... me diz que você também não aguenta mais usar essa propriedade?)
Temos:
Agora nós temos a integral de uma soma. Então devemos utilizar a propriedade que diz que a integral da soma é igual à soma das integrais:
Portanto, teremos:
Resposta
Exercício Resolvido #4
James Stewart Vol. I – 6ª ed. Exercício 47 da seção 5.2
Escreva como uma integral única na forma :
Passo 1
Temos que transformar a soma de 3 integrais em uma só.
Repare que as integrais possuem limites de integração diferentes e queremos transformar em uma só integral com limites de integração e .
Basicamente, temos que descobrir quem é e .
Passo 2
Nesses tipos de problemas, onde temos que manipular somente os limites de integração, vamos ter que usar as propriedades das integrais.
Ao olhar para as duas primeira integrais que compõem a soma, já podemos, de cara, usar uma propriedade de integrais definidas:
Nesse caso, temos:
Logo:
Observe que agora reduzimos um termo daquela soma, pois as duas primeiras integrais foram substituídas por uma única integral equivalente. O que temos agora é:
Passo 3
Agora, para podemos utilizar a mesma propriedade de antes, devemos lembrar da propriedade de inverter os limites de integração.
Nesse caso:
Assim, temos:
Agora, podemos utilizar novamente a seguinte propriedade:
Agora, temos:
Passo 4
Observe que a integral resultante tem limite inferior maior que o superior. Basta utilizarmos novamente a propriedade de inverter os limites de integração para reescrevê-la: