Teorema Fundamental do Calculo
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí, nós somos o Responde Aí e estamos aqui pra te ajudar nos sufocos do Cálculo! Hoje eu vou te apresentar o Teorema Fundamental do Cálculo!
O que é o Teorema Fundamental do Cálculo?
Sabe algumas operações inversas que a gente tem em matemática? Como por exemplo, a multiplicação é a operação inversa da divisão, ou então o logaritmo é a operação inversa da exponencial.
Esse é o espirito da coisa aqui! O Teorema Fundamental do Cálculo relaciona a integral com a derivada! A gente costuma dividir o Teorema fundamental do Cálculo em duas partes, a primeira é essa daqui:
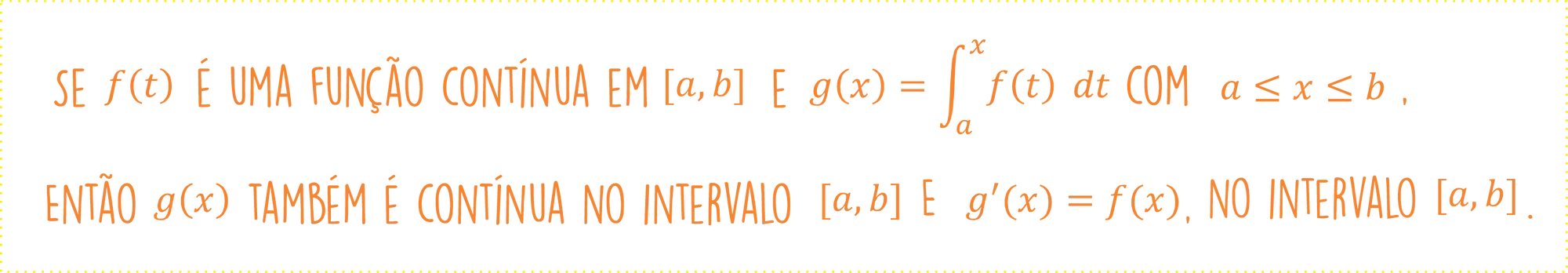
O que o teorema está dizendo é que se a função
Agora temos a parte 2 do Teorema Fundamental do Cálculo:

Ou seja, para encontrarmos a integral definida de
Ainda parece grego? Calma, confere esse videozinho aqui 👇👇👇
📢 Clique para ver mais:
Teorema Fundamental do Cálculo: Exemplo
Considere a seguinte função
Se quisermos calcular a derivada de
Vamos primeiro organizar as funções:
Se aplicarmos o teorema teremos que:
Basta pegarmos a função
Se liga que não é importante o limite inferior da integral, pode ser qualquer constante, e o limite superior deve ser o
Teorema Fundamental do Cálculo e a Regra da Cadeia
Imagina comigo a seguinte situação:
Aqui, ao invés do limite superior ser uma constante ela é uma função! Como podemos resolver isso?!
Primeiro nós teremos que definir duas novas funções:
Note que se eu faço
Para encontrarmos a derivada de
A derivada de
Mas como queremos
Agora, calculamos a derivada de
Agora, temos que substituir na expressão que achamos para
Parece meio confuso?
De forma geral, é só seguir esse quadrinho aqui:

Exercício: Seja
Agora bora praticar com mais exercícios?!