Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.4 - Ex. 16
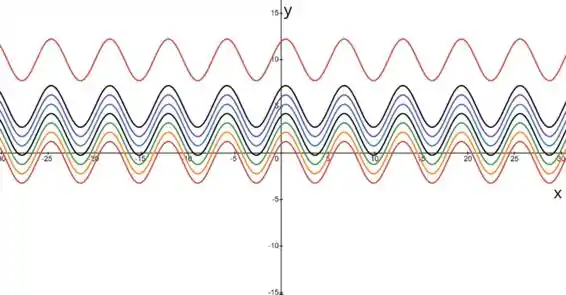
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela.
Passo 1
E aí? Blz?
A integral que ele nos pede para calcular é a seguinte:
Para isso vamos usar uma propriedade muito útil das integrais:
A integral da soma é a soma das integrais, dessa forma aqui:
Com isso já facilitamos a nossa vida, pois saímos em duas integrais que são tabeladas:
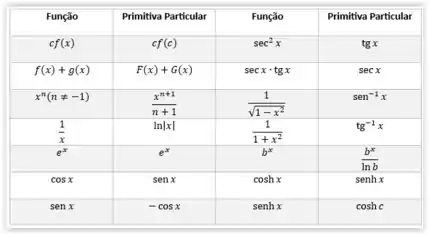
Tem apenas mais uma propriedade que vamos aplicar aqui, é que podemos tirar uma constante multiplicativa para fora da integral:
Agora sim, estamos prontos para resolver!
Passo 2
Separando em dois termos:
Tirando o da integral:
Olhando a tabela do passo 1:
Passo 3
Integrando, temos:
Logo,
Juntando as constantes:
Pra finalizar, vamos fazer o gráfico e para vários valores de . Olha só:
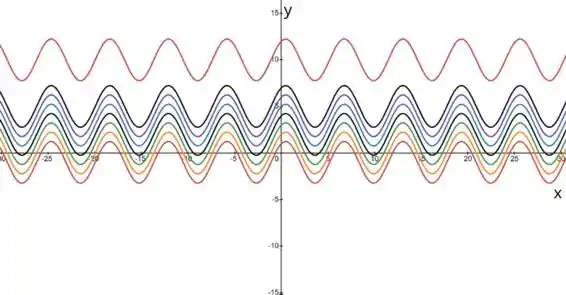
A aqui é bem simples, escolha um software para traçar o gráfico da função e fique colocando valores aleatórios para .
Resposta
