Indeterminação com Quociente de Polinômios
Produzido por Arthur Melo de AlmeidaTeoria
Faaala galera, da uma olhadinha aqui:
Opaaa, obtemos uma indeterminação , e por isso não podemos usar as propriedades. Maas, então como resolver o limite?
A ideia é a gente manipular o numerador e denominador, para que de algum modo a gente consiga sair dessa indeterminação que existe só pra complicar nossa vida.
Mas como fazemos isso ?
Vamos aplicar algumas ideias de fatoração que vimos no colégio. Por isso, vamos relembra-las hehe.
Fatoração de polinômios
- Fatoração de polinômio do grau por Bhaskara:
- Produtos notáveis:
- Briot-Ruffini:
Nós vamos ter em algum momento do nosso limite, uma equaçãozinha do segundo grau :
A ideia é que vamos aplicar Bhaskara, e descobrir as raízes e :
Depois de descobrir, vamos escrever sua forma fatorada no limite, que é :
Não esquece desse aí quando ele for diferente de !
Ex:
Se substituirmos o valor de 2, chegaremos novamente na indeterminação , assim observa que temos uma equaçãozinha do segundo grau no denominador :
Por Bhaskara, vamos descobrir nossas raízes :
Assim, e , escrevendo a forma fatorada :
Vamos substituir isso no nosso limite :
Note que podemos, simplificar:
Outra coisa que podemos usar é a ideia de produtos notáveis, os principais são :
Vamos pensar num exemplo :
Mais uma vez a indeterminação não deixa a gente simplesmente substituir. Mas podemos pensar nos produtos notáveis, como ?
Aqui vai uma gambiarra, vamos lembrar que :
E vimos pelos produtos notáveis que :
Então nosso denominador fica :
Colocando no nosso limite :
Simplificando :
É essa a ideia, você usa um produto notável para manipular o limite e sair da indeterminação.
Imagine que temos:
Para sair dessa indeterminação, dividimos numerador por denominador usando Briot-Ruffini:
Passo 1: Arme o quadro:
Escreva num quadro, como abaixo, os coeficientes do polinômio que se quer dividir alinhados do lado direito superior. A raiz do polinômio que dividimos deve estar do lado esquerdo superior. Já o primeiro coeficiente, do maior grau do polinômio, fica do lado direito inferior, logo abaixo de onde o escreveu em cima:
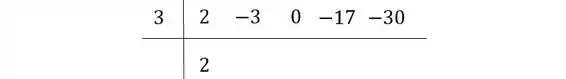
OBS.: Repare que colocamos um ali ocupando o espaço do grau . Para qualquer grau entre o grau máximo e o grau que tenha coeficiente nulo no polinômio, você precisa sempre escrever um no lugar do seu coeficiente.
Passo 2: Multiplique e some:
Multiplique a raiz pelo primeiro coeficiente, que você reescreveu embaixo ainda no passo 1, e some-o com o próximo coeficiente (nesse caso, ). Escreva o resultado embaixo do segundo coeficiente:
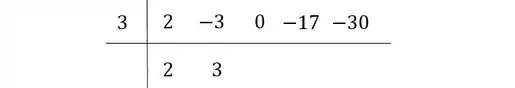
Passo 3: Repita:
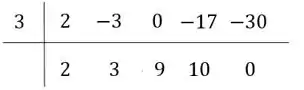
Passo 4: Junte:
Escreva o resultado com os coeficientes ordenados, sendo o primeiro que aparece na direita inferior aquele que acompanha elevado a e assim por diante até o penúltimo, que será o termo independente de , uma constante! O último termo é o resto da divisão:
Logo, podemos escrever:
Caso com módulo
Agora que você conhece como fazer a fatoração de termos polinomiais. Como fica se no limite aparecer um módulo?
Substituindo esse valor (pra variar...) teremos uma indeterminação . Agora a questão é fatorar esse cara de cima. Usando Bhaskara, a gente chega ao seguinte:
Ok, mas e esse módulo aí? Por definição, ele é dado assim:
Então vamos dividir a análise lateralmente também! Para valores maiores que será:
Para os valores menores que , por sua vez:
E, enfim, a gente vê que os limites laterais não batem e portanto o limite:
não existe!
Agora vamos aos exercícios!
Fatoração de polinômios
Caso com módulo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Resolva o limite:
Passo 1
Começando mais uma questão de limites, o primeiro passo é substituir o :
Passo 2
Indeterminação à vista, temos que arranjar um jeito de escapar da situação. Para isso, vou te lembrar de um negócio, produto notável conjugado:
Pensa comigo, nessa onda do produto notável, quem ali eu posso quebrar? O ilustríssimo !
Agora vamos reescrever o limite e ver o que sai.
Passo 3
Reescrevendo, ficamos com isso aqui:
Vou cortar o , ok?
Resultado em mãos, acabou a questão.
Resposta
Exercício Resolvido #2
UERJ – Cálculo 1 – Lista de Limites Professor Roger - 5
Calcule o limite abaixo usando as propriedades operatórias:
Passo 1
Ok, se substituirmos os valores:
É, deu ruim. Vamos ter que usar uma saída algébrica.
Passo 2
Bom, não é nada trivial pensar no que eu vou mostrar aqui de primeira, até porque não é um dos produtos notáveis mais importantes. Repara que , bem como . Apenas te mostrando que os de cima são o cubo dos debaixo.
Tem uma relação que amarra isso tudo:
Bom, no caso, eu posso abrir o termo de cima assim:
Passo 3
Basta levar isso para o limite em si e resolver:
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule o limite:
Passo 1
Rapaz, substituindo esse nós ficamos com uma indeterminação de . Nesse caso, vemos que é raiz dos dois caras. Vamos transformar o outro em um termo fatorado em função de .
Olha o termo do numerador, ele cai no produto notável do quadrado perfeito:
Assim, reescrevendo:
Passo 2
Repara, no denominador aquele módulo vai dar uma leve complicada na nossa vida. Não vai não, basta lembrar que o módulo vale ele mesmo quando é positivo e seu oposto quando é negativo. Nesse caso aqui, fica:
Logo, o limite vai depender se nos aproximamos pela direita ou pela esquerda de . O que isso significa? Que vamos ter que calcular o limite lateral para cada caso!
Passo 3
Para :
Para :
Enfim, o limite lateral bateu para uma constante, então temos um resultado.
Resposta
Exercício Resolvido #4
UERJ – Cálculo 1 – Lista de Limites Professor Roger - 6
Calcule o limite:
Passo 1
Então, estudante, se a gente jogar esse valor na criança vai ficar assim:
Bom, isso significa problema: teremos, então, que achar um jeito de solucionar isso.
Passo 2
Vamos lá, repara o seguinte, se zera os polinômios ali, significa então que ele é uma das raízes desse polinômio, né?
Então, vamos abrir esses polinômios aí para poder simplifica-los. O de cima é fácil, produto notável:
Ok, como era esperado o é uma das raízes! Para o outro (o de baixo), vamos de Bhaskara:
Assim, as raízes do polinômio serão:
Dessa maneira, abrindo o polinômio ele fica assim:
Passo 3
Reescrevo agora o polinômio todo:
Dá para cortar ali né?
Daí, peixe, é só substituir:
Resposta
Exercício Resolvido #5
Elaboração Própria
Calcule o limite:
Passo 1
A gente começa substituindo o limite, certo?
Deu ruim né? Então, vamos tentar usar uma malandragem algébrica.
Passo 2
Zerou em cima e embaixo, o que significa que vai aparecer na fatoração dos dois termos. Vamos dividí-los por esse termo, o de cima por Briot-Ruffini, o de baixo por Bhaskara.
Começamos com o de baixo:
Ou seja, .
OBS.: Esse aí veio por que nesse polinômio.
Passo 3
O de cima, dividimos ele por pelo método de Briot-Ruffini:
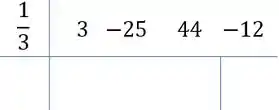
Desce o primeiro coeficiente:

Multiplicamos a raiz pelo primeiro e somamos ao segundo:
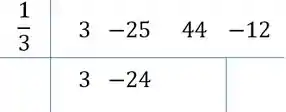
Repetimos isso para os dois outros números que restam:
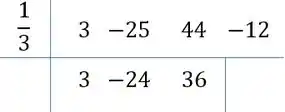
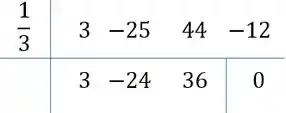
Ou seja, .
Passo 4
Substituindo no limite:
Na divisão de 2 frações, repetimos a primeira e multiplicamos pelo inverso da segunda:
Aplicando o MMC, achamos que:
Resposta
Exercício Resolvido #6
UFF, Cálculo IA-Lista 5, GMA, 2008-1, Questão 7.
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Subsituindo o você já percebe logo de cara que esse cara vai para uma indeterminação:
Bom, pra fugir disso a gente precisa fatorar esse cara. Mas calma aí, o bagulho tá elevado a ? Como eu faço isso??
Então, você não faz! Mas nós marotamente faremos algo que vai nos levar ao resultado, através de um padrão na fatoração.
Passo 2
Lembra que a dica para fatorar polinômios de grau maior ou igual a era usar Briot-Ruffini? Vamos lançar desse jeito então, tendo que o valor é e temos que dividir os dois polinômios por .
Repara ainda, para o polinômio de cima, que teremos no coeficiente de , em todos do grau até , no grau e o . Armando para o cara de cima fica assim:
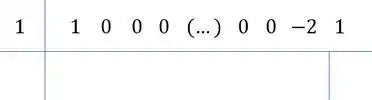
Mesmo esquema, desce o primeiro coeficiente, multiplica ele pela raiz, soma com o próximo coeficiente e assim por diante:
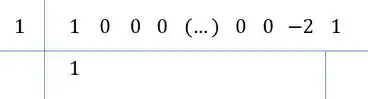
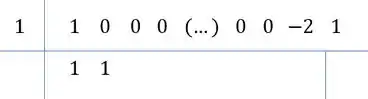
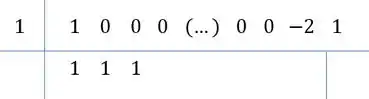
Repara, tem um padrão! Todos com ali vão ter coeficiente ao dividir!
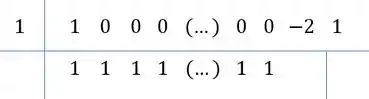
Continuando teremos:
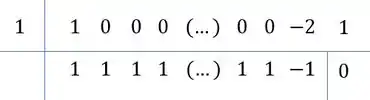
Ou seja, .
Passo 3
Não sei se você já se deu conta, mas para o cara debaixo, com o , vamos ter a mesma coisa! A diferença nesse caso é que os coeficientes zerados estarão só de até . Briot-Ruffini neles!
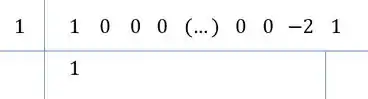
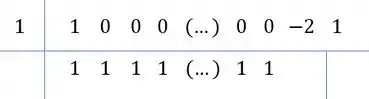
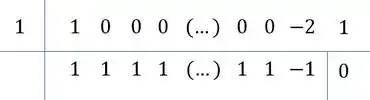
Ou seja,
Passo 4
Substituindo no limite, teremos:
Rapaz, repara nesse limite que sobrou! Lembra que elevado a qualquer número vai dar ? A gente vai ficar com números em cima e embaixo ao substituir , fora os dois que sobraram ali:
Questão trabalhosa e complicadinha, heim?