Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 28e

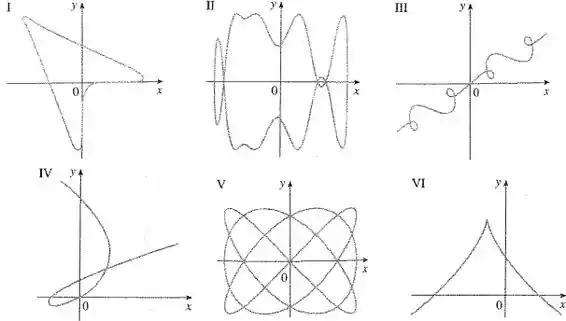
Ligue as equações paramétricas aos gráfico de I-VI.

Passo 1

Olá, me amigo. Vamos resolver essa atividade juntos.

A questão fornece uma curva parametrizada e pede para identificarmos o seu gráfico.

Nesse caso,

Para corresponder o gráfico com as funções, precisamos observar como as funções se comportam em alguns valores especiais.

Podemos olhar as raízes, os limites , devemos observar esses pontos e assim poderemos escolher o gráfico que melhor se enquadra.

Passo 2

Vamos procurar interseções com eixos.

Fazendo :

Isso acontece para o ângulo do seno é igual a zero, então:

E nesse caso:

Assim, a curva corta o eixo no ponto .

Outra informação que podemos obter, é que o gráfico é simétrico em relação à linha:

Porque:

Portanto, o Gráfico I é o gráfico que representa esta equação paramétrica.

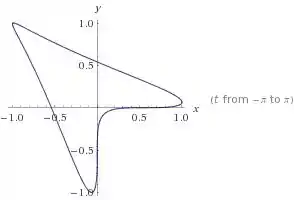
Resposta

I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta.Elimine o parâmetro para encontrar uma equação cartesian

Elimine o parâmetro para encontrar uma equação cartesiana da curva.Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o prametro aumenta. x = 1 2 cos ⁡ θ ,y = 2 sen ⁡ θ ,

Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de θ em coordenadas cartesianas. r = c o s( 5 θ )

Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de θ em coordenadas cartesianas. r = 1 - c o s θ

Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de θ em coordenadas cartesianas. r = 1 + 2 c o s θ