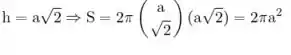Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.8 - Ex. 10
10. Cilindro em uma esfera Encontre o raio e a altura do cilindro circular reto aberto de maior área de superfície que pode ser inscrito em uma esfera de raio a. Qual é a maior área de
superfície?
Passo 1
Fala galerinha tranquilidade, vamos fazer uma aplicação do que estamos fazendo nessa bateria de exercício, primeiro vamos otimizar a função assim:
Com a opitimização, do volume e da superfície, podemos encontrar o gradiente das funções:
Passo 2
Aqui vamos encontrar o parâmetro lambda:
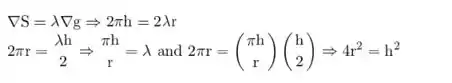
Passo 3
Aqui podemos chegar na altura e no raio:
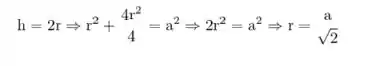
Resposta
Exercícios de Livros Relacionados
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
Determine os valores extremos de f sujeita a ambas as restrições. f x , y , z = x 2 + y 2 + z 2 , x - y = 1 , y 2 - z 2 = 1
Encontre o valor mínimo de f x , y , z = x 2 + 2 y 2 + 3 z 2 sujeito a restrição x + 2 y + 3 z = 10 . Mostre que f não tem valor máximo com essa restrição.
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
O método dos multiplicadores de Lagrange assume que os valores extremos existem, mas esse nem sempre é o caso. Mostre que o problema de encontrar o valor mínimo de f x , y = x 2 + y 2 sujeito a restri