Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.8 - Ex. 8
Passo 1
Fala galerinha tranquilidade, nesse caso vamos seguir os passos semelhantes ao que fizemos nas questões anteriores com a regrinha dos gradientes, e do paramêtro lambda:
Paro o item (a)
Pela regra temos:
Passo 2
Aqui vamos encontrar o parâmetro lambda:
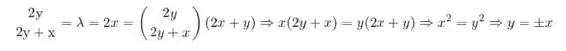
Passo 3
Caso 1
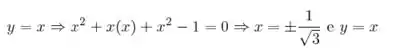
Caso 2
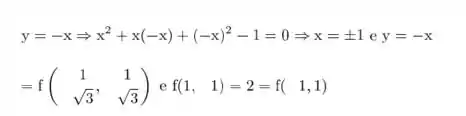
Resposta
Os pontos mais distantes são e
Os pontos mais próximos são
Exercícios de Livros Relacionados
Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.Exercício 51
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.Exercício 42
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita