Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 11

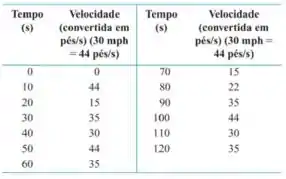
11. Comprimento de uma estrada Você e um amigo estão prestes a dirigir em um trecho sinuoso de uma estrada de terra em um carro cujo velocímetro funciona, mas cujo hodômetro (contador de quilômetros) está quebrado. Para descobrir a extensão desse trecho de estrada, você registra a velocidade do carro a intervalos de 10 segundos, com os resultados apresentados na tabela a seguir. Estime o comprimento desse percurso usando

a. o valor na extremidade esquerda de cada intervalo.

b. o valor na extren1idade direita de cada intervalo.

Passo 1

Só precisamos aplicar na fórmula, apresentada no capitulo.

Vamos dizer que a velocidade se mantém constante, até que termine cada subintervalo. Após isso a velocidade vai aumentar para o próximo valor da tabela e continuar constante durante o subintervalo, até o próximo valor e assim sucessivemente até acabar os valores da tabela.

Usando os valores da extremidade esquerda:

Passo 2

Usando os valores da extremidade direita:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ - π / 3 2 π / 3 cos ⁡ xd x (Teorema dado no livro)

Prove o Teorema 5.6.2.:Se f for definida no intervalo fechado [ a , b ] , e se lim Δ → 0 ⁡ ∑ i = 1 N f ξ i Δ i x existe, onde Δ é qualquer partição de [ a , b ] , então se k for uma constante qualquer

Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ - 2 1 x + 1 2 / 3d x (Teorema dado no livro)

Calcule a integral definidaint_2^(- 1) 3 x ( x - 4 ) d x usando os resultados:int_(- 1)^2 x^2 d x = 3 int_(- 1)^2 x d x = (3)/(2)

Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ π / 6 π / 3 sen ⁡ xd x (Teorema dado no livro)