Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 11
11-22 Encontre os pontos x, se houver, nos quais f não é contínua.
11-
Passo 1
Gente, supomos que p(x) seja um polinômio e a um número real qualquer, então:
Isso quer dizer que os polinômios são contínuos em toda parte.
Passo 2
Outra forma de ver isso é através do gráfico da função. A função está definida para todos os reais.
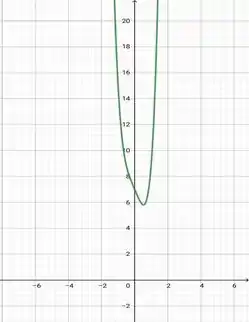
Resposta
f é contínua em todos os pontos.
Exercícios de Livros Relacionados
1-8 Encontre os pontos de descontinuidade, se existirem.6.f x = 1 1 + s e n 2 x
17-40 Encontre os limites.18. lim x → + ∞ s e n ( π x 2 - 3 x )
1-8 Encontre os pontos de descontinuidade, se existirem.4. f ( x ) = s e c x
17-40 Encontre os limites.30. lim x → 0 s e n 2 x 3 x 2
17-40 Encontre os limites.26. lim θ → 0 s e n 2 θ θ