Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 13
11-22 Encontre os pontos x, se houver, nos quais f não é contínua.
13-
Passo 1
Gente, nós sabemos que essa é uma função racional, e funções racionais são contínuas em cada ponto em que o denominador não se anula e tem descontinuidade nos pontos em que o denominador é zero.
Nesse caso, o denominador nunca será zero, já que .
Passo 2
Outra forma de ver isso é através do gráfico da função. A função está definida para todos os reais.
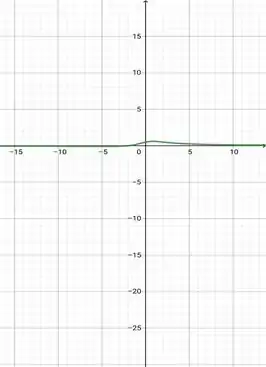
Resposta
f é contínua em todos os pontos.
Exercícios de Livros Relacionados
9-14 Determine onde f é contínua.11- f x = ln a r c t g x x 2 - 9
43-46 Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.43- Suponha que uma função f satisfaça f x + 5 ≤x + 1 Com qualquer número real x . Então lim x → - 1 f ( x ) = - 5 .
41-42 (a) Complete a tabela e dê uma estimativa para o limite indicado. (b) Encontre o valor exato do limite.41- f x = s e n x - 5 x 2 - 25 ; lim x → 5 f ( x )
49- Encontre um valor diferente de zero para a constante k que torne f ( x ) t g k x x ,x0 3 x + 2 k 2 , x ≥ 0 Contínua em x = 0 .
15-16 Em cada parte, use o Teorema 1.5.6 (b) para mostrar que a função é contínua em toda parte.15- a) s e n ( x 3 + 7 x + 1 ) b) s e n x c) cos 3 ( x + 1 )