Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 40
40. Prove que é contínua em toda parte, justificando cuidadosamente cada passo.
Passo 1
Primeiro, vamos analisar a função dada no enunciado. Se trata de uma função racional com uma raiz quadrada no denominador. Agora, nós devemos nos perguntar se existe algum ponto no qual a nossa função não esteja bem definida. Ou seja, se para algum o denominador se anula ou se a raiz quadrada fica negativa. Esses são os pontos em que a nossa função dá problema.
Passo 2
Agora, vamos ver se o denominador da nossa função se anula em algum ponto.
Para tanto, vamos definir
Assim, teremos
Igualando o polinômio acima a zero,
Como é menor do que , vamos obter duas raízes negativas. Portanto, não existirá que satisfaça a eq. (1) para cada um dos valores de y obtidos a partir de (2).
Com isso, vemos que o denominador nunca se anula.
Passo 3
Agora, precisamos nos certificar de que a raiz nunca fica negativa. Para isso, vamos ter auxílio do gráfico da função .
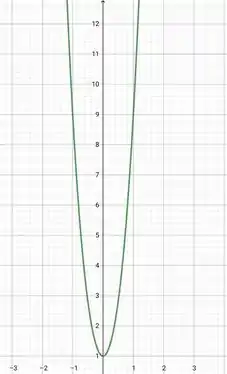
Ao analisar o gráfico, vemos que a função só assume valores positivos.
Portanto, não temos problema com a raiz quadrada.
Resposta
Mostramos, nos passos anteriores, que a função não tem nenhuma singularidade, nenhum ponto em que ela não esteja bem definida. Portanto, ela é contínua em toda parte.