Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.1 - Ex. 51
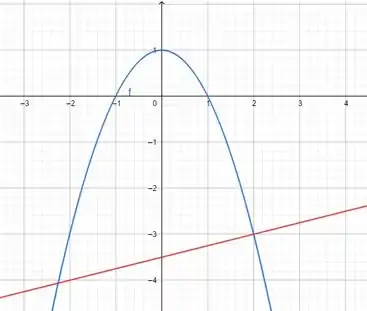
51. A reta normal à curva C em um ponto P é, pela definição, a reta que passa por P e é perpendicular à reta tangente a C em P. Ache uma equação da reta normal à parábola no ponto . Esboce a parábola e sua reta normal.
Passo 1
Opa, bora lá! Vamos primeiro achar a reta tangente nesse ponto e veremos a relação entre a reta tangente e a reta normal.
Lembra que o coeficiente angular da reta tangente é a derivada da reta no ponto .
Passo 2
Vamos lá! Fazer a derivada:
Substituindo o , pela abscissa do ponto .
Lembra da sua aula de Geometria Analítica? Tem uma relação entre o coeficiente angular de duas retas perpendiculares! Você lembra essa relação?
Não????
Tudo bem, vou colocar aqui:
Chamaremos de o coeficiente angular da primeira reta e o coeficiente angular da primeira reta. E as duas são perpendiculares!
Passo 3
Com a relação já escrita ali em cima! Vamos calcular o coeficiente angular da reta normal (perpendicular)
E a equação da reta é assim, de forma geral hein!
Agora o gráficoo! Estamos acabandoo!
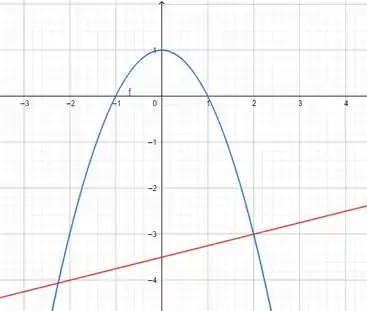
Prontinho!
Resposta
