Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 13
12.(a) Encontre a inclinação da tangente à parábola nos pontos onde .
(b) Encontre as inclinações das retas tangentes nos pontos cujas coordenadas são e
(c) Faça o gráfico da curva e das tangentes em uma tela comum.
Passo 1
Olá, meu querido aluno. Pronto para mais uma resolução?
Veja bem, aqui iremos encontrar a inclinação de uma reta tangente à curva:
Tudo isso, em um ponto genérico . É valido lembrar que esse ponto genérico pertence a nossa curva .
Para que possamos encontrar essa equação da reta, deveremos encontrar o coeficiente angular da reta tangente. Encontramos ele com a seguinte relação:
Em que , é o coeficiente angular da reta tangente à curva no ponto e .
Com o ponto em mão, podemos substituir ele na relação abaixo, para encontrarmos finalmente a equação:
Onde são os pontos dados para a gente e que pertencem a nossa reta. Costumeiramente as questões dizem, ‘encontra a equação da reta tangente a curva e que passe pelo ponto ’, então já fique ligado.
Passo 2
Letra a)
Primeiramente, vamos então descobrir a inclinação da reta tangente:
Vamos realizar alguns cálculos fora da equação enrolarmos:
Desenvolvendo o produto notável:
Substituindo tudo no cálculo do limite temos:
Simplificando os termos:
Botando o em evidência para fazermos a redução depois:
“Cortando” o de cima e de baixo, temos:
Agora temos o que nos foi pedido, o coeficiente angular no ponto .
Passo 3
Letra b)
Agora apenas substituiremos o valor de pelos valores do enunciado, que será a abscissa dos pontos do enunciado.
Então!! Só jogaremos esse valor no que calculamos:
Faremos a mesma coisa para o outro ponto.
Porém, agora o muda. Seu valor no ponto é .
Passo 4
Letra c)
Vamos agora finalizar nossa resolução encontrando as equações das retas tangentes e que passam pelos pontos e
Substituindo os dados:
- Primeiro para
- Agora para
Podemos agora gerar o grafico com a nossa curva e suas retas tangentes:
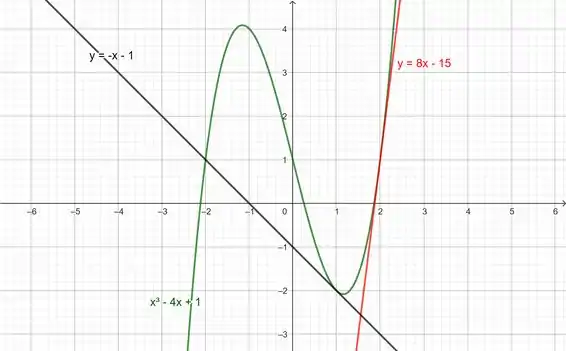
Resposta
()
(c) O gráfico.
