Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.1 - Ex. 42
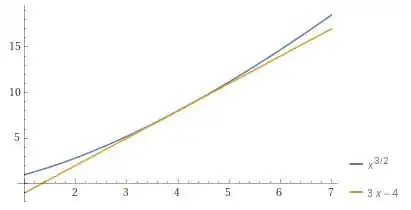
41-42 Ache uma equação da reta tangente à curva no ponto dado. Ilustre fazendo o gráfico da curva e a reta tangente sobre a mesma tela;
42.
Passo 1
Faala galerinha,
Nessa questão queremos encontrar a equação da reta tangente à curva para um ponto dado. A nossa curva é dada por:
E para escrevermos a equação da reta tangente vamos usar a seguinte equação:
Onde e são as coordenadas do ponto onde queremos traçar a reta tangente.
E é a inclinação da função no ponto dado. Ou seja, a derivada da função.
E para fechar, vamos plotar o gráfico da função e da reta tangente para ver se deu tudo certo.
Passo 2
Vamos começar dando uma ajeitada na nossa função, para que calcular a derivada dela seja mais fácil.
Passo 3
Agora vamos encontrar a nossa derivada .
Lembra a interpretação da derivada?
É o coeficiente angular da reta tangente, o mesmo que a inclinação da reta tangente.
Então o coeficiente angular da reta tangente, no ponto , é:
Passo 4
E a equação da reta tangente a um gráfico é dada por:
O ponto de tangência é o .
Então:
Para finalizar, faremos os dois gráficos juntos, dessa forma!!
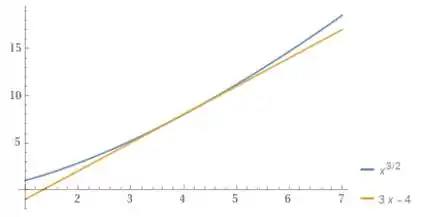
Resposta
