Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 12
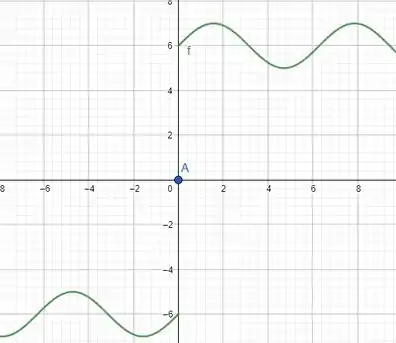
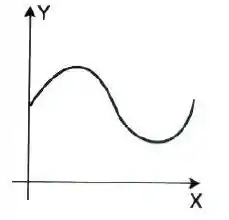
12.Seja uma função, cujo gráfico para tem o aspecto indicado na figura. Completar esse gráfico no domínio de , se:
a) é par;
b) é impar;
Passo 1
Você lembra qual a propriedade gráfica de funções pares e ímpares?
Nas funções pares o gráfico é simétrico em relação ao eixo .
Nas funções impares o gráfico é simétrico em relação a origem.
Passo 2
Vou colocar um exemplo de função par e te mostrar o gráfico feito no geogebra, assim você vai perceber melhor essa propriedade.
Uma ideia!!! Sempre que tiver que usar funções pares ou impares utilize para funções pares e para funções impares.
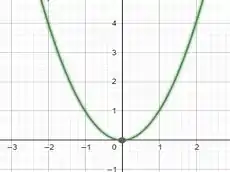
Simétrico em relação ao eixo .
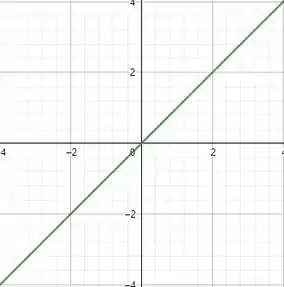
Simétrico em relação à origem.
Passo 3
Então para fazermos o gráfico da função par, temos que completar esse gráfico sendo simétrico em realção ao eixo .
O gráfico seria mais ou menos assim:
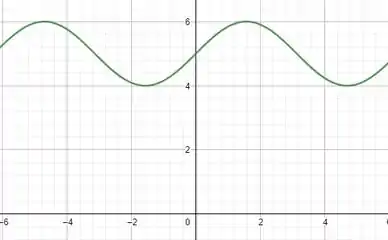
Então para fazermos o gráfico da função impar, temos que completar esse gráfico sendo simétrico em relação a origem.
O gráfico seria mais ou menos assim:
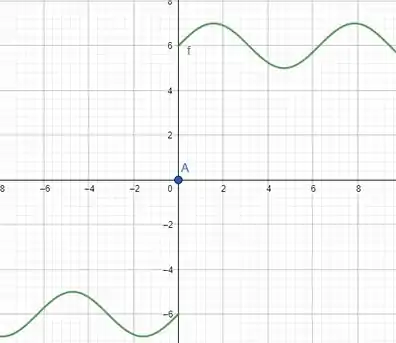
Resposta
(a)
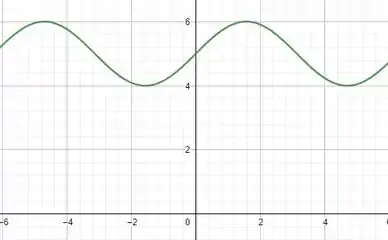
(b)
