Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 13d
13.Em cada um dos exercícios determine a fórmula da função inversa. Fazer os gráficos da função dada e da sua inversa.
(d) ,
Passo 1
Temos um método para determinarmos a função inversa. Esse método consiste em mudarmos o e de lugar e isolarmos o . Faremos matematicamente para ficar mais fácil visualização.
Passo 2
Trocaremos por
Agora precisamos isolar .
Oraaa a função inversa é a mesma que a função, não há problema veremos quando desenharmos o gráfico que essa função é simétrica em relação a reta .
Então a função inversa, que denotamos por , é
Passo 3
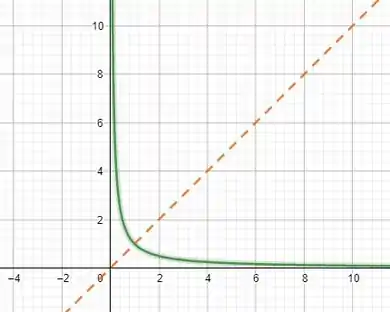
Faremos o gráfico da função ,em verde, sua inversa, em azul e colocaremos também a função , porém desenharemos o gráfico pontilhado e em vermelho.
Por que colocaremos a função ???
Porque a função e a sua inversa são simétricas em relação a função .
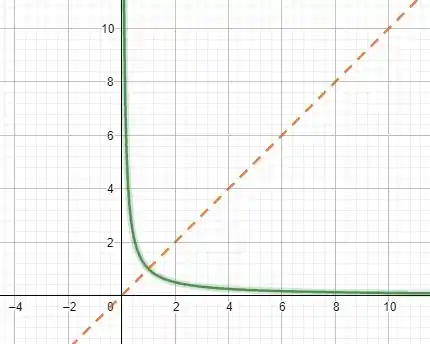
A própria função é simétrica em relação ao reta , isso afirma que a lei da função inversa é igual a lei da função direta.
Resposta
