Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 13
13. O ciclo limite encontrado no Problema 12 aparece como resultado de uma bifurcação de Hopf em um valor de c entre e . Determine, ou pelo menos estime com mais precisão, o valor de . Existem diversas maneiras de fazer isto.
(a) Desenhe trajetórias para diversos valores de c.
(b) Calcule os autovalores nos pontos críticos para diversos valores de c.
(c) Use o resultado do Problema 3(b) anterior.
Passo 1
Aqui não existe muito mistério, neh? Vamos pegar valores de entre e , digamos... e , substituir no código do exercício 11 e colocar o programa pra rodar! As trajetórias que vamos fazer aqui serão tridimensionais, e para isso vamos usar as mesmas plotagens de exercícios anteriores (11 e 12)!
Vamos lá?
Passo 2
Com o e de a , com o ponto inicial em ...
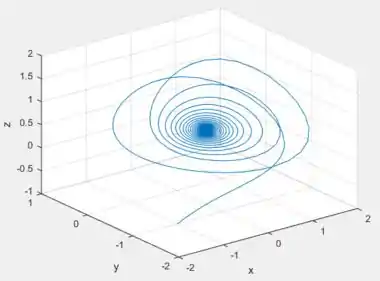
OPA! Convergiu!
Agora com ...
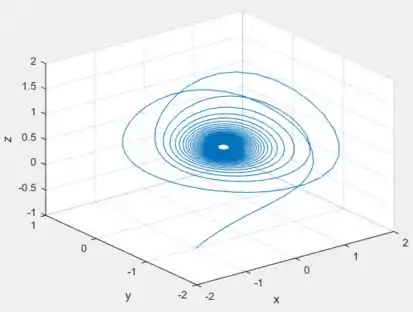
Ta convergindo também, mas bem lentamente, percebe?
Agora e com ?
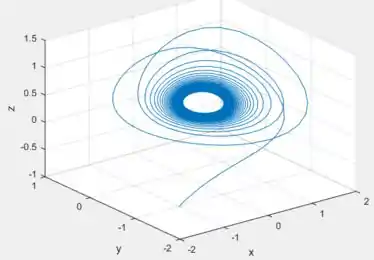
Parou de convergir para a estabilidade . O que existe um ponde de bifurcação entre e . Saca?
Passo 3
Vamos lá, para ... De acordo com o exercício anterior, podemos determinar o ponto crítico através das três equações a seguir:
Com ...
Resolvendo essa equação do segundo grau com um auxílio de uma calculadora...
O outro valor não é interessante para análise por gerar um autovalor inteiramente positivo. Logo, os valores de e de do ponto será...
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
Passo 4
Com ...
Resolvendo essa equação do segundo grau com um auxílio de uma calculadora...
Logo, os valores de e de do ponto será...
O ponto nesse caso é:
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
Passo 5
Poxa, então para , obtivemos autovalores com a parte real negativa:
Já para , o autovetor já possui um valor real positivo:
O que faz a solução se tornar instável e em ressonância. Ou seja, existe um ponto de bifurcação entre e .
Passo 6
O jacobiano em termos de é...
Calculando então o determinante disso aí...
SHOW! Bem, simplificar isso, vai ser um pouco complicado. Por isso vamos usar o WolframAlpha para fazer isso chegando a:
Ou, dando mais uma arrumadinha...
Vimos no exercício 3 que o ponto de bifurcação acontece quando...
Então aqui teremos...
A solução no Wolfram desse problema é:
Como tiramos da equação...
Logo...
Que jogando na calculadora, nos dá mais ou menos , que é o ponto onde acontece a bifurcação .
Resposta
Ei, a resposta está no passo a passo :)