Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 13
13. Queda livre e resistência do ar Um objeto é solto de um helicóptero. O objeto cai cada vez mais rápido, mas sua aceleração (taxa de variação da velocidade) diminui com o passar do tempo por causa da resistência do ar. A aceleração é medida em pés por segundo ao quadrado e registrada a cada segundo durante 5 segundos após o lançamento, como se pode ver na tabela a seguir:.
a. Faça uma estimativa superior para o módulo da velocidade quando .
b. Faça uma estimativa inferior para o módulo da velocidade quando .
c. Faça uma estimativa superior para a altura da queda quando .
Passo 1
a.
Como se trata de uma estimativa superior, vamos usar os valores que ficam acima do gráfico, no caso:
Passo 2
b.
Já nesse caso, é uma estimativa inferior, logo vamos usar os valores que ficam abaixo do gráfico:
Passo 3
c.
Para que a gente possa fazer uma estimativa da altura da queda, precisamos dos valores das velocidades. Fazendo as estimativas superiores para o valor de cada velocidade nos tempos 1, 2 e 3 vamo obter:
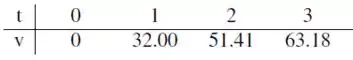
Agora sim podemos fazer a estimativa superior da altura:
Resposta
a.
b.
c.