Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 14
14- Princípio de Cavalieri Um sólido está situado entre planos perpendiculares ao eixo em e . As seções transversais perpendiculares ao eixo são discos circulares cujos diâmetros vão da reta à reta , conforme mostra a figura a seguir. Explique por que o sólido tem o mesmo volume que um cone circular reto com raio de base 3 e altura 12.
Passo 1
Planificando as funções escritas acima temos:
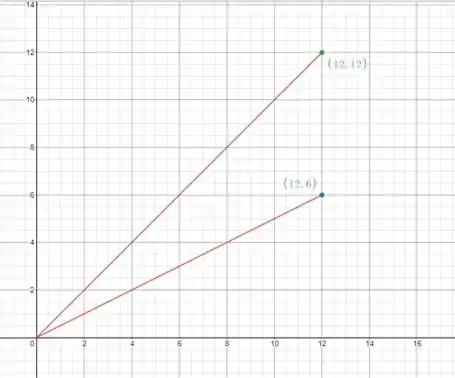
O que nos dá um círculo de base com raio igual a 3 e altura igual a 12.
Passo 2
Assim como se fossemos plotar um gráfico de cone sem distorção teríamos a seguinte imagem.
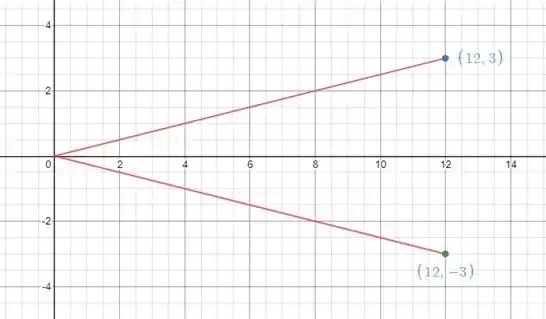
Passo 3
Como os dois cones tem a mesma altura e o mesmo raio, logo pelo princípio de Cavalieri podemos dizer que os dois sólidos têm o mesmo volume.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre o volume do sólido S descrito.A base de S é um disco circular de raio r . Secções transversais paralelas, perpendiculares à base, são quadradas.
Escreva uma integral para um toro sólido (o sólido com formato de rosquinha da figura) com raios r e R .Interpretando a integral como uma área, encontre o volume do toro.
Ache o volume comum aos dois cilindros circulares, cada qual com raio r , se os eixos dos cilindros se interceptam em ângulos retos.
Um buraco de raio r é perfurado pelo centro de uma esfera de raio Rr . Encontre o volume da porção remanescente da esfera.