14.1. O mapa de contorno mostra a precipitação média de neve (em polegadas) perto do Lago Michigan. Estime o valor da derivada direcional da função da precipitação de neve em Muskegon, Michigan, na direção de Ludington. Quais são as unidades?

Oie, meu amigo. Vou te ajudar a resolver essa atividade.

A questão pede para a gente estimar a derivada direcional da função de precipitação em Muskegon, na direção de Ludington.

Queremos encontrar o valor da função da precipitação de neve. Uma forma de fazer isso é imaginar uma linha que passar por Mukesgon e Ludington.

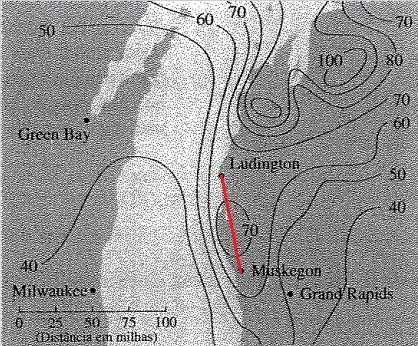
Agora podemos usar essa linha para ver o como a média de precipitação de neve vai mudando.

Repare que pelos dados que temos, um ponto perto de Muskegon, tem a média de polegadas, enquanto outro ponto próximo de Muskegon, só que mais perto de Ludington, tem polegadas.

Em outras palavras, quando estamos indo na direção a Ludington pela linha que traçamos a precipitação de neve muda de para .

E usando a escala da imagem podemos aproximar a distância entre essas duas marcações para milhas.