Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 43
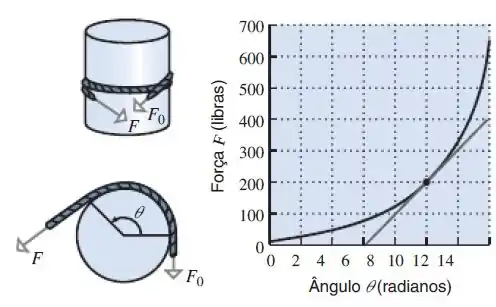
É fato que, quando uma corda flexível é enrolada em um cilindro áspero, uma pequena força de magnitude em uma ponta pode resistir a uma grande força de magnitude na outra ponta. O tamanho de depende do ângulo , segundo o qual a corda é enrolada em torno do cilindro (veja a figura a seguir). Essa figura mostra o gráfico de (em libras) versus (em radianos), onde é a magnitude da força à qual resiste uma força com libras de magnitude para uma certa corda e um certo cilindro.
- Estime os valores de e de quando for de radianos.
- Pode ser mostrado que a força satisfaz a equação , onde a constante é denominada coeficiente de atrito. Use os resultados de a) para estimar o valor de .
Passo 1
- Analisando o gráfico, nós vemos que quando a força é igual a .
- Para estimar o valor de é simples, vamos substituir os valores que achamos em:
Já para estimar vamos achar a inclinação nesse ponto usando:
Onde e são pontos da reta tangente, vamos substituir então:
Passo 2
Vamos lá:
Resposta
- e
Exercícios de Livros Relacionados
Encontre f ' ( a ) . f x = 4 1 - x
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. G t =1 - 2 t 3 + t
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. f x = x 3 2
Use a definição de derivada para encontrar f ' x ef ' ' ( x ) . A seguir, trace f ,f ' ef ' ' , e em uma mesma tela e verifique se suas respostas são razoáveis. f x = x 3 - 3 x
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. f x = x 2 - 1 2 x - 3