Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 16
Valéria dirige em uma auto-estrada. Esboce o gráfico da função posição do carro, se ela dirigir da seguinte maneira: no instante , o carro está no ponto onde o marcador de milha mostra e viaja a uma velocidade constante de milhas por hora. Continua com essa velocidade por exatamente hora. Então gradualmente com o carro vai diminuindo a velocidade em um período de minutos, quando Valéria para pra jantar. O jantar dura minutos e, assim, então ela recomeça a viagem aumentando gradualmente a velocidade até milhas por hora em um período de 2 minutos. Ela dirige a milhas por horas e, então, num período de minutos, gradualmente para completamente o carro.
Passo 1
Fala aí. Tudo certinho com você?
Bom, essa questão descreve o percurso de Valeria com seu carro em uma auto-estrada e pede para que a gente esboce um gráfico da função posição do carro com o passar do tempo.
O próprio enunciado vai nos contando a posição, a velocidade e o tempo desse percurso em diferentes momentos. Então vamos usar essas informações passo a passo para construir esse gráfico.
Passo 2
Primeiro vamos escolher as unidades e os eixos. O problema quer a função posição com o passar do tempo. As posições indicadas então em milhas, já o tempo está sendo dado em unidades diferentes no enunciado, temos momentos sendo descritos em horas e outros em minutos. Para que isso não gere confusão, vamos usar uma unidade única, que aqui será o minuto.
E nosso eixo será:
Passo 3
Inicialmente, Valéria sai do ponto correspondente a 15 milhas e anda por 1 hora com uma velocidade constante de .
Passando essa velocidade para , ficamos com
Esse é um movimento uniforme que pode ser descrito pela função horária:
Logo seu gráfico será a reta crescente descrita para o intervalo de . Assim, nosso gráfico se torna:
Passo 4
Após esse tempo, Valéria começa a diminuir gradualmente sua velocidade por minutos até para completamente seu carro. Ou seja, ela passa a desenvolver um movimento desacelerado para que sua velocidade varie de para .
E sua aceleração será:
E a equação horária de posição para esse intervalo de será:
Como esse movimento começa em , precisamos fazer um deslocamento de 60 unidade na função, e ela se torna:
Como são só 2 minutinhos, a curva é bem pequenininha, e a distância final desse percurso é , o que dá aproximadamente.
Vou dar um zoom pra gente conseguir ver:
É esse pedacinho vermelho aí do gráfico.
Passo 5
Após parar, Valéria fica parada para jantar. Com isso nosso gráfico será uma reta horizontal no intervalo de .
Passo 6
Depois disso, ela recomeça sua viagem aumentando gradualmente a velocidade até , que é igual a , em um intervalo de . O que resulta em um movimento acelerado dado por:
E a equação horária de posição para esse intervalo de será:
Como esse movimento começa em , precisamos fazer um deslocamento de 88 unidade na função, e ela se torna:
Como , pois ela estava parada, teremos:
Como, novamente, são só 2 minutinhos, a curva é bem pequenininha, e a distância final desse percurso é .
Passo 7
Após atingir essa velocidade, Valéria mantém a velocidade constante de , durante horas, ou melhor, . Isso nos dará um movimento uniforme no intervalo de com:
Com ajuste de minutos, teremos:
Passo 8
Finalmente, Valéria diminui sua velocidade por gradualmente até parar. Isso faz com que o gráfico de seu movimento se torne desacelerado com:
para que sua velocidade varie de para .
E sua aceleração será:
E a equação horária de posição para esse intervalo de será:
Como esse movimento começa em , precisamos fazer um deslocamento de 210 unidade na função, e ela se torna:
Como são só 2 minutinhos, a curva é bem pequenininha, e a distância final desse percurso é , o que dá aproximadamente.
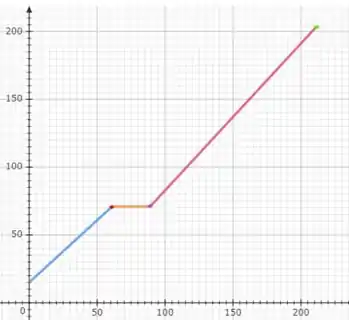
E prontinho, esse é o gráfico do movimento de Valéria. Ainda podemos afirmar que ela percorreu . O que dá .
E isso é tudo.
Resposta
