O Gateway Arch em St. Louis foi projetado por Eero Saarinen e contruído usando a equação
para a curva central do arco, em que e são medidos em metros e .
- Trace a cruva central.
- Qual é a altura do arco em seu centro?
- Em quais pontos a altura é m?
- Qual é a inclinação do arco nos pontos da parte (c)?
Passo 1
Fala galera, nessa questão temos a equação de um arco que é dada por:
Daí, vamos usar uma calculadora gráfica para traçar esse arco, sabendo que o módulo de é menor ou igual a
Logo, está entre e .
Então, com uso do gráfico, podemos encontrar a altura do arco no seu centro, podemos usar a equação para encontrar em quais pontos a altura é e por fim, encontrar a inclinação nesses pontos usando a derivada dessa expressão.
Bora lá?
Passo 2
Vamos lá, para a letra a) queremos o gráfico da curva
seria no seguinte formato:
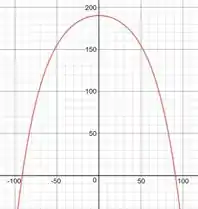
Passo 3
Na letra b), vemos que a altura máxima ocorre em , logo, basta substituir na expressão:
Temos que para calcular precisamos da fórmula:
Assim, temos então que:
Então temos que a altura do arco em seu centro �� m.
Passo 4
Para achar os pontos, devemos fazer :
Temos que calcular , para isso precisamos da fórmula:
Vamos substituir então:
Então, os pontos em que a altura é m são:
e
Passo 5
Para calcular a inclinação devemos derivar a expressão:
Então:
Vamos usar inicialmente a regra da subtração:
Para derivar o primeiro termo vamos usar a regra da constante:
Assim, ficamos com:
Já o segundo termo vamos usar algumas regras, a fórmula da derivada de funções hiperbólicas inversas, da multiplicação por constante e da função , além da famosa regra da cadeia.
Vamos aplicar as regras então:
Vamos agora voltar a expressão original:
Nosso próximo passo é calcular , que fica fácil ao sabermos das fórmulas abaixo:
e
Passo 6
Vamos substituir:
E por último é só substituir nos pontos que achamos na letra (c):
Assim, a inclinação em é e a inclinação em é 3,6.
Resposta
-
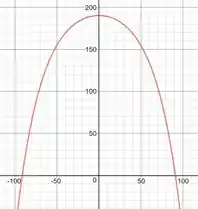
- m
- e
- Em é e em é 3,6