Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.6 - Ex. 22
17-40 Encontre os limites.
22.
Passo 1
Como a funções cosseno e arcotangente são contínuas em toda parte, segue que
Passo 2
Agora, vamos analisar o gráfico da função para entendermos o que acontece quando
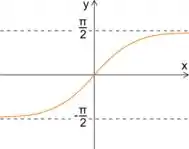
A função vai para
Assim, vemos que
Resposta
Exercícios de Livros Relacionados
Encontre os valores para os quais f é descontínua. Em quais desses pontos f é contínua pela direita, pela esquerda ou nenhum dos dois casos? Desenho o gráfico de f .
Encontre os valores para os quais f é descontínua. Em quais desses pontos f é contínua pela direita, pela esquerda ou nenhum dos dois casos? Desenho o gráfico de f .
Para f x = x ln x :Faça um gráfico de f ( x ) , sabendo:(i) lim x → 0 + f x = 0 (ii)lim x → 1 - f x = - ∞ (iii)lim x → 1 + f x = ∞ (iv)lim x → ∞ f x = ∞
Determine, se existirem, os pontos onde as seguintes funções não são contínuas. f x = 3 - x 6 - x
Determine, se existirem, os valores de x ∈ D f , nos quais a função f x não é contínua. f x = 1 + cos x 3 + sen x