Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 42
Encontre os valores para os quais é descontínua. Em quais desses pontos é contínua pela direita, pela esquerda ou nenhum dos dois casos? Desenho o gráfico de .
Passo 1
Olá, vamos para mais uma resolução?
Aqui a gente tem uma função determinada por várias equações, cada uma para um intervalo, e nos é perguntado em quais valores nossa função é descontinua.
Além disso, devemos também descobrir quais pontos a nossa função é continua pela direita, ou pela esquerda, ou apenas é continua mesmo.
Para conseguirmos resolver essa, a gente primeiro precisa definir o que é continuidade.
Em termos mais formais, uma função é contínua em um ponto se os seguintes critérios forem atendidos:
1. está definido.
2. O limite de quando se aproxima de a partir de ambos os lados é igual a . Matematicamente, isso é expresso como:
3. A função está definida para todos os pontos em um intervalo aberto em torno de .
Em outras palavras, não há saltos, lacunas ou quebras abruptas nos gráficos de funções contínuas. Elas podem ter curvas suaves, linhas retas ou até mesmo funções mais complexas, mas a característica essencial é que elas não têm descontinuidades.
Então iremos aqui analisar se nossa função esta de acordo com os critérios, e assim decidir se ela é ou não continua.
Passo 2
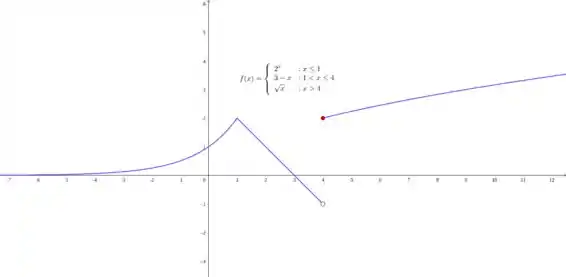
Nesse exercício iremos analisar a seguinte função:
Note que:
- é continua em por ser uma função exponencial;
- é continua em por ser uma função exponencial;
- é continua em por ser uma função raiz.
Agora, calculando os limites laterais de para o ponto , temos:
Calculando para a esquerda:
Calculando para a direita:
Agora precisamos calcular para sabermos se a função é realmente continua pela direita e pela esquerda.
então é contínua no ponto , tanto pela direita quanto pela esquerda.
Passo 3
Agora, calculando os limites laterais de para o ponto :
Calculando pela esquerda:
Calculando pela direita:
Agora precisamos calcular para sabermos se a função é realmente continua pela direita e pela esquerda.
Como temos que
então é descontínua em pois os limites laterais são diferentes, sendo assim seu limite neste ponto não existe, mas é contínua pela esquerda nesse ponto.
O gráfico da função é mostrado a seguir:
Resposta
