Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 15
Paraquedismo. Se um corpo de massa que cai sob a ação da gravidade, desde o repouso, encontra uma força de resistência do ar proporcional ao quadrado da velocidade, então, a velocidade do corpo após segundos em queda satisfaz a equação
onde é uma constante que depende das propriedades aerodinâmicas do corpo e da densidade do ar. (Supomos que a queda é muito breve para ser afetada por variações na densidade do ar.)
a. Desenhe uma reta de fase para a equação.
b. Esboce uma curva de velocidade típica.
c. No caso de um paraquedista com libras de peso () e com o tempo em segundos e a distância em pés, um valor típico de é . Qual é a velocidade terminal do paraquedista? Repita o procedimento para um paraquedista com 200 libras de peso.
Passo 1
Para esboçarmos uma reta de fase para a equação precisamos primeiramente achar os pontos de equilíbrio, ou seja, os pontos onde . Assim,
Dividindo todo mundo por temos
Para avaliarmos a concavidade teremos que calcular a segunda derivada, dessa forma
Então, nossa reta de fase será
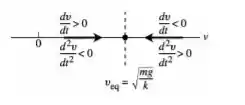
Passo 2
A reta de velocidade típica é uma curva crescente que vai até uma reta assintótica horizontal que é a velocidade terminar dada por . Dessa forma, nossa curva fica esboçada da seguinte forma
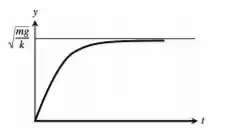
Passo 3
Para calcularmos a velocidade terminal, basta substituirmos os valores dados na equação, assim
Resposta
Ei, a resposta está no passo a passo :)