Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 18
18. Explique por que a função é descontinua no número dado . Esboce o gráfico da função.
Passo 1
Opa, vamos fazer essa questão! O enunciado nos dá:
E pede pra a gente explicar porque a função é descontínua em .
Beleza, sabemos que uma função é contínua se:
Pra isso acontecer devemos obedecer três condições:
- deve existir, ou seja tem que pertencer ao domínio da função ;
- existe, ou seja, deve ser um número pertencente aos números reais;
- .
Pra resolver esse problema vamos calcular:
E depois vamos verificar se os requisitos acima são obedecidos! Depois disso a gente vai esboçar o gráfico de e verificar graficamente a nossa conclusão sobre a continuidade!
Passo 2
Temos a seguinte função:
O nosso limite é:
Ué, mas no ponto a função não é igual a ?!
Sim, mas aqui a gente tá tendendo a , não estamos exatamente nesse ponto! Vamos resolver o limite:
Ops, se quando nos aproximamos do nosso ponto vamos pro infinito, isso significa que o limite não existe! Portanto a função não é contínua em .
Vamos olhar primeiro a parte da função onde temos definido:
Como a função é uma constante, temos:
Não precisamos nem nos preocupar em olhar limites laterais, o limite vai ser sempre igual a ! Agora vamos olhar os limites laterais da segunda condição:
Quando estamos vindo pela esquerda, estamos pegando valores muito próximos de 2, porém menores que ele. Logo, dará um numero muito pequeno, mas negativo. Assim:
Já quando nos aproximamos pela direta, pegamos valores um pouco maior. Logo, será muito próximo de 0 e positivo. Portanto:
Passo 3
Agora, esboçando o gráfico, temos:
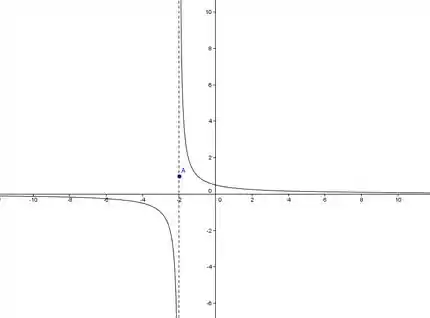
Quando desenhamos um gráfico de uma função contínua, não precisamos tirar o lápiz do papel, o que não é o nosso caso nessa função!
Resposta
- A função é descontínua.
- Esboço do gráfico.