Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 28c
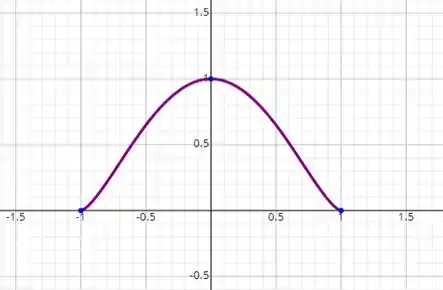
28. Dada (a) Prove que é contínua no intervalo fechado (b) Prove que é derivável no intervalo aberto e que ambas existem. (c) Faça um esboço do gráfico de .
Letra ( c)
Passo 1
O esboço do gráfico da função pode ser obtido utilizando o programa de computador Symbolab Assim, o esboço do gráfico da função é:
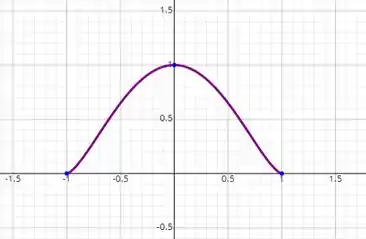
Resposta
Exercícios de Livros Relacionados
Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .
Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .
Suponha f derivável no intervalo I . Prove que se f for estritamente crescente em I , então f ' x ≥ 0 em I .
Suponha f derivável em a ,b e tal que f ' a ∙ f ' b0 . Prove que existe p em ] a ,b [ tal que f x ≤ f p para todo x em a ,b ou f x ≥ f p para todo x em a ,b . Interprete geometricamente.
Suponha f derivável em a ,b tal que f ' a ∙ f ' b0 e f a = f b . Prove que existem x 1 ,x 2 ∈] a ,b [ tais que, para todo x em ] a ,b [ , f x 1 ≤ f x ≤ f x 2 . Interprete geometricamente.