Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 85
(a) Use um gráfico para conjecturar o valor do limite
(b) Use um gráfico da sequência na parte (a) para encontrar os menores valores de que correspondam a e na Definição .
Passo 1
Fala aí, galera! Tudo certinho??
Nessa questão precisamos primeiro usar um gráfico para conjecturar o limite da nossa sequência
E depois encontrar os menores valores de que correspondam a e na Definição . E o que diz a definição 2? Ela nos diz que:
Uma sequência tem limite se, para cada , existir um inteiro correspondente tal que, se , então .
Deu pra dar aquela assustada?
Calma! Não precisa se desesperar porque vamos fazer tudo com calma e bem devagar! Beleza?!
Passo 2
Vamos começar calculando alguns pontos para entender melhor o comportamento e ajudar a plotarmos o gráfico.
Para :
Para :
Para :
Para :
Para :
Parece que dá uma crescida e depois uma diminuída, né? Vamos calcular mais alguns valores pra ver se o comportamento de diminuir continua...
Para :
Para :
Para :
Para :
parece que a sequência converge pra , né mesmo? Vamos plotar o gráfico dessa sequência pra visualizar melhor.
Passo 3
(a) Olhando pro gráfico da sequência:
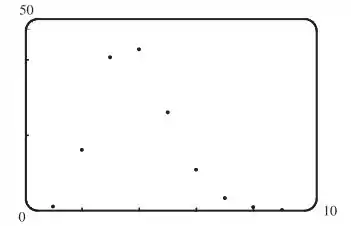
Observando, esse gráfico, parece que realmente a sequência converge pra , né mesmo? Então:
Passo 4
(b) Agora precisamos Encontrar os menores valores de que correspondam a e na Definição .
Vamos relembrar o que essa definição nos diz? De acordo com a Definição ,
Uma sequência tem limite se, para cada , existir um inteiro correspondente tal que, se , então .
Calma! Vamos traduzir de acordo com a sequência do enunciado:
Para provar que o limite de quando tende ao infinito é zero, precisamos mostrar que,
Para cada , existe um inteiro tal que, se, então , ou seja, .
Melhorou? hehe
Então vamos aplicar a definição para encontrar os menores valores de que correspondem a e :
No nosso caso o nosso limite L tende a zero () como visto no item (a), então
Agora olha esse gráfico:
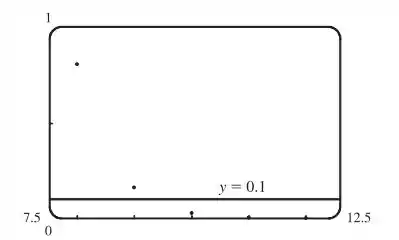
Observando ele, dá um parecer que o menor valor possível de correspondente a é , pois quando , mas . Beleza?
Agora olha esse outro gráfico:
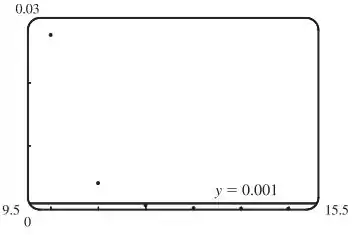
Assim, para , o menor valor possível de é , já que quando .
Resposta
(a)
(b)