19-22. Calcule, com quatro casas decimais, os primeiros 10 termos da sequência e use-os para traçar o gráfico da sequência com a mão. Esta sequência parece ter um limite? Se assim for, calcule-o. Se não, explique o por quê.
20.
Passo 1
Fala Aí! Tudo certinho? Vamos lá! Essa questão nos pede 3 coisas:
- Calcular os 10 primeiros termos da sequência.
- Traçar o gráfico da sequência.
- Verificar se a sequência tem um limite.
Vamos então atacar cada um desses 3 pontos!

Passo 2
Primeiramente devemos descobrir quando vale os primeiros termos da sequência. Para descobrirmos isso, basta substituirmos por . Isso é bem tranquilo de fazer, não é mesmo? Sendo assim, teremos:
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Show?!
Passo 3
Agora que descobrimos os 10 primeiros termos da sequência, vamos colocar esses pontos em um gráfico. Se fizermos isso, teremos:
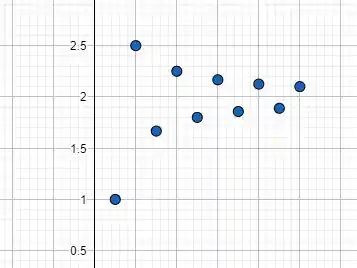
Passo 4
O último ponto pedido é para verificarmos se a sequência tem um limite.
Se observarmos o gráfico com atenção, notaremos que a sequência aparenta se aproximar de , não é mesmo? Então sim, a sequência aparenta ter um limite! Sendo assim, devemos calcular o limite dessa sequência para comprovarmos a observação!
Como a expressão é uma soma, podemos separar os limites, utilizando a propriedade da soma dos limites:
Sabemos que o limite de uma constante é a própria constante. Então, o limite de é . Mas quanto ao segundo limite, qual é seu resultado? Vamos analisar com mais calma:
- Quando olhamos para , o denominador está crescendo à medida que avançamos na sequência. Isso significa que o termo geral está sendo dividido por números cada vez maiores. Concorda?
- Por outro lado, o numerador alterna entre e conforme aumenta.
Por exemplo, quando é , a fração é
Para :
e assim por diante. Conforme cresce, a magnitude do numerador não aumenta, mas o denominador sim, e isso faz com que a fração como um todo se aproxime de .
Assim, embora o numerador esteja oscilando, o denominador está crescendo mais rapidamente, e isso leva a a convergir para à medida que tende ao infinito.
Ou seja,
Portanto,
Portanto, o limite da sequência quando tende ao infinito é . Isso significa que a sequência tem uma assíntota horizontal em .
Resposta
Os 10 primeiros termos da sequência são: , , , , , , , , , .
O gráfico da função é
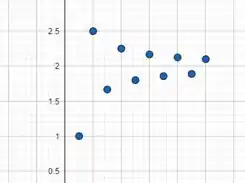
O limite da sequência quando tende ao infinito é . Isso significa que a sequência tem uma assíntota horizontal em .