Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 1e
1-Encontrar, se existirem, os pontos de máximo e de mínimo globais das funções:
a)
Passo 1
Galera, a primeira coisa que temos que fazer é encontrar os pontos críticos dessa função. Para identificar esses pontos temos que resolver o seguinte sistema:
Ou seja, as derivadas parciais da função z = f(x,y) tem que ser iguais a zero.
Passo 2
Dessa forma, temos que:
Assim,
Logo, temos os seguintes de x e y para pontos críticos:
X = e
Y = e
Gente, os ângulos de e são os valores de x para os quais o cosseno é zero, assim como os ângulos de e são os valores de y para os quais o seno é zero. Dessa forma, temos os seguintes pontos críticos:
, ),
OKKKKK, mas a questão não para aí. A questão pediu pra gente determinar os pontos máximos e mínimos, bom, nós já vimos que essa função tem um ponto crítico, agora nos resta saber se ele é máximo ou mínimo.
Passo 3
Para determinarmos os pontos máximos e mínimos temos que usar a matriz hessiana:
Assim, temos que :
e
Afinal, o que isso quer dizer ????
Bom, como e , então é um ponto de máximo local de f.
e , então é um ponto de mínimo local de f.
Passo 4
De acordo com o gráfico da função apresentada abaixo, podemos perceber que os máximos e mínimos locais também são globais.
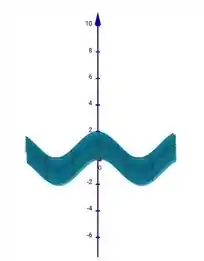
Resposta
é um ponto de máximo global de f.
é um ponto de mínimo global de f.