Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 1f
1.Encontrar, se existirem, os pontos de máximos e de mínimos globais das funções:
f)
Passo 1
Vamos começar calculando as derivadas parciais:
Igualando a zero, teremos:
Daí, segue que (x,y)=(0,0).
Como as derivadas parciais de primeira existem em todo (, não há nenhum outro ponto crítico além do que já encontramos.
Passo 2
Calculando as derivadas parciais de segunda ordem:
Como é de classe , ou seja, as derivadas de todas as ordens existem e são contínuas (isso pode ser observado, pois não há nenhuma singularidade na nossa função, nenhum ponto em que ela não esteja bem definida, sacou ?!), sabemos que
Aplicando o teste da segunda derivada parcial:
Oooopss!!!! Nós sabemos que quando , o teste é inconclusivo. E agora ????
Calma, garoto. Vem comigo que vai dar certo.
Perceba que o gráfico da função dada no enunciado coincide muito com a superfície do parabolóide circular a não ser pelo e que deveriam ser e , respectivamente.
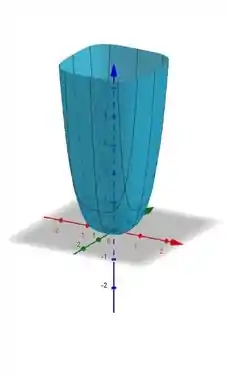
Se você olhar para imagem, vai perceber que não existem máximos globais, pois o gráfico da nossa função cresce infinitamente. Mas perceba que (0,0) é ponto de mínimo global, pois (0,0,0) é o ponto mais baixo do nosso gráfico.
Resposta
Existe um único ponto de mínimo global: (0,0). Não existem máximos globais.