Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 20
20. Ache, por meio de um corte, o volume do tetraedro com três faces mutuamente perpendiculares e três arestas mutuamente perpendiculares, cujos comprimentos são 3, 4 e 7cm.
Passo 1
Vamos entender como esse tetraedro está disposto, fazer o corte e depois usar a fórmula do volume aplicado pro cone.
Passo 2
O tetraedro será como na figura, o corte será o triângulo perpendicular ao eixo , e fica a unidades da origem. Sendo que o lado de 3cm fica sobre o eixo , o lado de 4cm sobre o eixo e o lado de 7cm sobre o eixo .
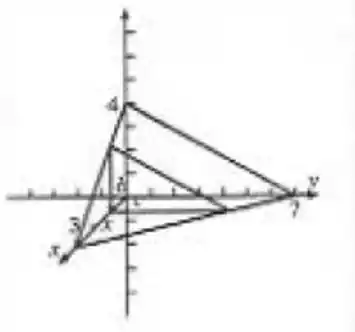
Esse triângulo do corte tem altura e largura . Por semelhança de triângulos com as face do tetraedro, temos e
Isolando e teremos a altura e a base, que serão e .
Passo 3
Pela definição 6.1.1 temos
No nosso caso, como vimos antes, a área do triângulo será ...
(lembrando que vai de 0 até 3)
Passo 4
Agora, vamos resolver essa integral:
Prontinho, esse é o volume em