21. Inscreva um polígono regular de lados dentro de um círculo de raio 1 e calcule a área do polígono para os seguintes valores de :
a. 4 (quadrado)
b. 8 (octógono)
c. 16
d. Compare as áreas obtidas nos itens (a), (b) e (c) com a área do círculo.
Passo 1
a.
Vamos desenhar o quadrado dentro do circulo:
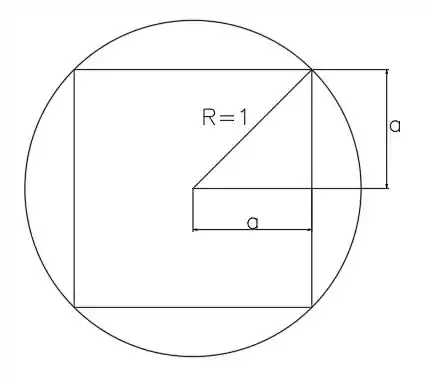
No desenho eu chamei o lado daquel triangulo de , então o lado do nosso quadrado vale , consequentemente a área do quadrado vale:
Passo 2
Para descobirmos quanto vale a área, precisamos descobrir quanto vale . E isso é fácil só usar pitagoras naquele triângulo, em que a hipotenusa dele é igual ao raio do circulo:
Prontinho, agora é só substituir na equação da área do quadrado:
Passo 3
b.
Vamos fazer a mesma coisa da letra (a), desenhar o octógono dentro do circulo:
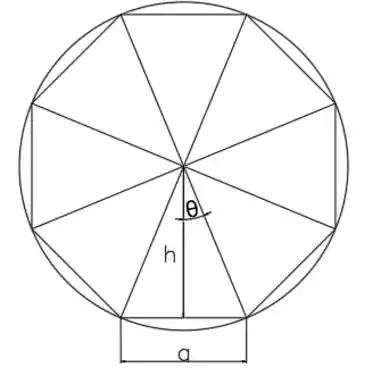
Perceba que vamos ter 8 triângulos isósceles iguais dentro desse octógono, vamos calcular a área de um deles e multiplicar por 8 para descobrirmos a área total.
A área de uma triângulo é igual a
Se desenharmos todos os ângulos um do lado do outro, vamos perceber que precisamos de 16 angulos para completarmos uma volta inteira, . Ou seja,
O lado maior do triângulo é igual ao raio do circulo.
A altura do triângulo é igual ao lado maior do vezes o cosseno de :
Já a metade da base do triângulo é igual ao lado maior vezes o seno de :
Com isso descobrimos a área do triângulo:
E a área do octógono será:
Passo 4
c.
Como nas duas ultimas letras, vamos desenhar o polígono dentro do criculo:
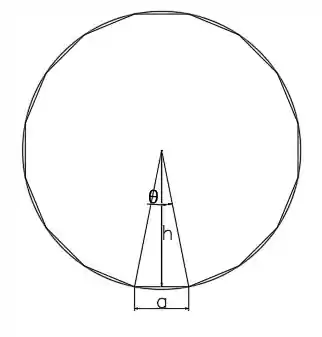
Nesse caso nós vamos ter 16 triângulos isósceles e vamos usar do mesmo método anterior para calcular sua área.
Diferente da letra (b) em que precisamos de 16 ângulos somados para conseguirmos os 360°, aqui vamos precisar de 32, então:
O lado maior do triâgulo continua sendo igual ao raio.
E a altura e base são calculadas da mesma forma:
e
Sua área vai ser de:
E a área do polígono:
Passo 5
d.
A área do circulo é
seu raio é 1, então:
Podemos observar que as áreas dos polígonos são menores que a área total do círculo, mas a medida que o numero de lados desses poligonos cresce, mais a área do polígono se aproxima da área do círculo.
Resposta
a.
b.
c.
d. A medida que o numero de lados desses poligonos cresce, mais a área do polígono se aproxima da área do círculo.