Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 21
21.Use considerações de simetria para argumentar que o centroide de um triângulo isósceles fica na mediana da base do triângulo.
Passo 1
O centroide de uma região é o centro de gravidade dessa região.
Passo 2
Vamos começar desenhando esse triângulo isósceles qualquer, mas para melhorar vou colocar um vértice na origem!!!
Passo 3
Precisamos traçar uma reta que divida esse triângulo em dois iguais, uma reta de equilíbrio, pois o centroide vai estar nessa reta!
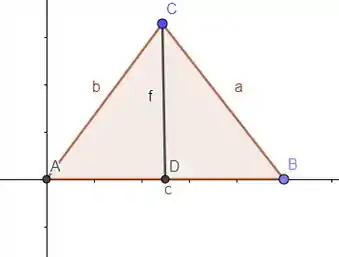
Essa reta divide esse triângulo em dois iguais, então o segmento tem de ser igual ao segmento !!
O único segmento que faz com que seja igual a é a mediana!!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Desenhe o conjunto A dado e calcule a área:A é o conjunto do plano limitado pelas retas x = 1, x = 4, y = 0 e pelo gráfico de y = √ x .
Desenhe o conjunto A dado e calcule a área:A é o conjunto do plano limitado pela y = x, pelo gráfico de y = x³, com - 1 ≤ x ≤ 1 .
Desenhe o conjunto A dado e calcule a área:A é o conjunto de todos (x, y) tais que 0≤ y ≤4 - x ² ².
Desenhe o conjunto A dado e calcule a área:A = { ( x ,y ) ∈ R ² ∣ x0 ² e x 3 - x ≤ y ≤ - x 2 + 5 x } .
Desenhe o conjunto A dado e calcule a área:A é o conjunto de todos (x, y) tais que x 2 - 1≤ y≤ 0 .