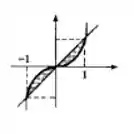
Desenhe o conjunto A dado e calcule a área:
A é o conjunto do plano limitado pela y = x, pelo gráfico de y = x³, com .
Passo 1
Lembre-se: para desenhar a figura basta colocar os dados do problema, um de cada vez. O conjunto se encontra sempre entre as funções dadas e marcá-lo no desenho ajuda a visualizar e calcular.
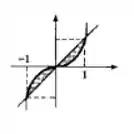
Passo 2
A partir do desenho fica mais simples de montar a equação de área. É possível observar, pela simetria do gráfico, que a área abaixo do primeiro trecho de curva é igual à segunda área. Assim:
Resposta