22.Use considerações de simetria para argumentar que o centroide de uma elipse fica na interseção dos semieixos da elipse.
Passo 1
Vamos começar desenhando essa elipse.
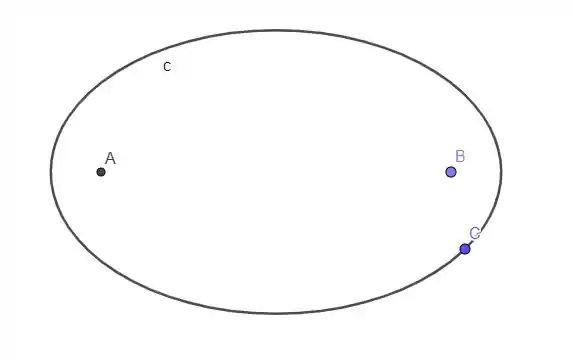
Passo 2
Vamos começar traçar o semieixo em e vermos se a elipse ficará simétrica em relação a esse semieixo !!
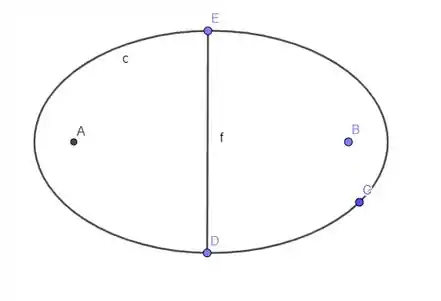
Tudo o que está a direita é igual a tudo que está a esquerda, então a elipse é simétrica em relação ao semi eixo !!
Como o semi eixo é uma reta de equilíbrio, já que a elipse é simétrica em relação a esse segmento!!
Isso quer dizer que o centroide está nesse semi eixo
Passo 3
Agora faremos a mesma coisa, porém para o semi-eixo
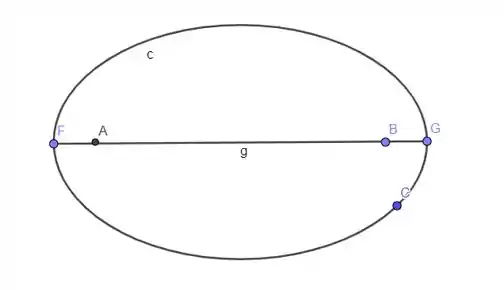
Tudo o que está acima é igual a tudo que está abaixo, então a elipse é simétrica em relação ao semi eixo !!
Como o semi eixo é uma reta de equilíbrio, já que a elipse é simétrica em relação a esse segmento!!
Isso quer dizer que o centroide está nesse semi eixo
Como o centroide tem de estar no semi eixo e no semi eixo ao mesmo tempo, então ele está na interseção desses dois semieixos da elipse.
Resposta
Ei, a resposta está no passo a passo :)